
分析 由已知数列递推式可得${a}_{n+1}=3{a}_{n}+{2}^{n-1}$,然后利用等比数列的定义可得数列{Sn+2n}是等比数列;求出等比数列的通项公式,代入Sn=$\frac{{a}_{n+1}}{2}$-2n-1,可得n≥2时数列{an}的通项公式an=2(t+2)•3n-2-2n-1,验证首项不成立,说明②错误;再利用作差法,化为关于n的函数,可得使an+1≤an成立和使an+1≥an成立的t的取值范围.
解答 解:①∵Sn=$\frac{{a}_{n+1}}{2}$-2n-1,
∴$\frac{{S}_{n}+{2}^{n}}{{S}_{n-1}+{2}^{n-1}}=\frac{\frac{{a}_{n+1}}{2}-{2}^{n-1}+{2}^{n}}{\frac{{a}_{n}}{2}-{2}^{n-2}+{2}^{n-1}}$,
∵${S}_{n}-{S}_{n-1}=\frac{{a}_{n+1}}{2}-{2}^{n-1}-\frac{{a}_{n}}{2}+{2}^{n-2}$=$\frac{{a}_{n+1}-{a}_{n}}{2}-{2}^{n-2}$,
∴${a}_{n+1}=3{a}_{n}+{2}^{n-1}$,代入$\frac{{S}_{n}+{2}^{n}}{{S}_{n-1}+{2}^{n-1}}=\frac{\frac{{a}_{n+1}}{2}-{2}^{n-1}+{2}^{n}}{\frac{{a}_{n}}{2}-{2}^{n-2}+{2}^{n-1}}$,
可得$\frac{{S}_{n}+{2}^{n}}{{S}_{n-1}+{2}^{n-1}}=3$,
∴数列{Sn+2n}是等比数列,故①正确;
②∵数列{Sn+2n}是等比数列,且${S}_{1}+{2}^{1}={a}_{1}+2=t+2$,
∴${S}_{n}+{2}^{n}=(t+2)•{3}^{n-1}$,则${S}_{n}=(t+2)•{3}^{n-1}-{2}^{n}$,
${S}_{n-1}=(t+2)•{3}^{n-2}-{2}^{n-1}$(n≥2),
∴当n≥2时,${a}_{n}=2{S}_{n-1}+{2}^{n-1}$=2(t+2)•3n-2-2n+2n-1=2(t+2)•3n-2-2n-1,
验证首项不成立,故②不正确;
③${a}_{n}=2(t+2)•{3}^{n-2}-{2}^{n-1}$,${a}_{n+1}=2(t+2)•{3}^{n-1}-{2}^{n}$,
若an+1≤an,则2(t+2)•3n-1-2n-2(t+2)•3n-2+2n-1=4(t+2)•3n-2-2n-1≤0,
即$4(t+2)≤\frac{{2}^{n-1}}{{3}^{n-2}}=2•(\frac{2}{3})^{n-2}$,∴t+2<0,则t<-2,故③错误.
④由③知,an+1≥an,则$4(t+2)≥2•(\frac{2}{3})^{n-2}$,4(t+2)≥3,即t$≥-\frac{5}{4}$,故④错误.
∴说法正确的是①②.
故答案为:①.
点评 本题考查命题的真假判断与应用,考查了数列递推式,考查了等比关系的确定,考查数列的函数特性,考查计算能力,是难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(cm) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 49 | 46 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(cm) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y(码) | 42 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
| 高个 | 非高个 | 合计 | |
| 大脚 | |||
| 非大脚 | 12 | ||
| 合计 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
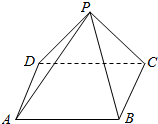 已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ex+2 | B. | ex-2 | C. | ex+2 | D. | ex-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)是R上的奇函数,且x>0时,f(x)=-x2+2x.
已知函数f(x)是R上的奇函数,且x>0时,f(x)=-x2+2x.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | a<b<c | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com