
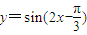 µÄĶ¼ĻóĻņ×óĘ½ŅĘ
µÄĶ¼ĻóĻņ×óĘ½ŅĘ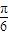 øöµ„Ī»£¬ŌŁ½«ŠĀŗÆŹżµÄÖÜĘŚĄ©“óĪŖŌĄ“µÄĮ½±¶£¬ŌņĖłµĆĶ¼ĻóµÄŗÆŹż½āĪöŹ½ĪŖy=sinx£®
øöµ„Ī»£¬ŌŁ½«ŠĀŗÆŹżµÄÖÜĘŚĄ©“óĪŖŌĄ“µÄĮ½±¶£¬ŌņĖłµĆĶ¼ĻóµÄŗÆŹż½āĪöŹ½ĪŖy=sinx£® £©2+
£©2+ ”Ż0³ÉĮ¢
”Ż0³ÉĮ¢ £©2+
£©2+ ”Ż0ĪŖÕęĆüĢā£¬ŌņĆüĢāp”ÄqŹĒÕęĆüĢā£¬¢ŁÕżČ·
”Ż0ĪŖÕęĆüĢā£¬ŌņĆüĢāp”ÄqŹĒÕęĆüĢā£¬¢ŁÕżČ·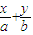 =1£¬ÓÉÖ±Ļß¹ż£Ø-1£¬2£©æɵĆa=1£¬ŌņÖ±Ļß·½³ĢĪŖx+y-1=0£¬
=1£¬ÓÉÖ±Ļß¹ż£Ø-1£¬2£©æɵĆa=1£¬ŌņÖ±Ļß·½³ĢĪŖx+y-1=0£¬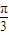 £©µÄĶ¼ĻóĻņ×óĘ½ŅĘ
£©µÄĶ¼ĻóĻņ×óĘ½ŅĘ 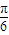 øöµ„Ī»æɵĆŗÆŹży=sin2xµÄĶ¼Ļó£¬ŌŁ½«ŠĀŗÆŹżµÄÖÜĘŚĄ©“óĪŖŌĄ“µÄĮ½±¶£¬æɵĆĶ¼ĻóµÄŗÆŹż½āĪöŹ½ĪŖy=sinx£®¢ÜÕżČ·
øöµ„Ī»æɵĆŗÆŹży=sin2xµÄĶ¼Ļó£¬ŌŁ½«ŠĀŗÆŹżµÄÖÜĘŚĄ©“óĪŖŌĄ“µÄĮ½±¶£¬æɵĆĶ¼ĻóµÄŗÆŹż½āĪöŹ½ĪŖy=sinx£®¢ÜÕżČ·

 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø Äæ±ź²āŹŌĻµĮŠ“š°ø
Äæ±ź²āŹŌĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A”¢£Ø1£©£Ø2£©£Ø3£© |
| B”¢£Ø2£©£Ø3£©£Ø4£© |
| C”¢£Ø1£©£Ø3£©£Ø4£© |
| D”¢£Ø1£©£Ø2£©£Ø4£© |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼ĖłŹ¾£¬Õż·½ĢåABCD-A”äB”äC”äD”äµÄĄā³¤ĪŖ1£¬E”¢F·Ö±šŹĒĄāAA”䣬CC”äµÄÖŠµć£¬¹żÖ±ĻßEFµÄĘ½Ćę·Ö±šÓėĄāBB”䔢DD”ä½»ÓŚM”¢N£¬ÉčBM=x£¬x”Ź[0£¬1]£¬øų³öŅŌĻĀĖÄøöĆüĢā£ŗ
ČēĶ¼ĖłŹ¾£¬Õż·½ĢåABCD-A”äB”äC”äD”äµÄĄā³¤ĪŖ1£¬E”¢F·Ö±šŹĒĄāAA”䣬CC”äµÄÖŠµć£¬¹żÖ±ĻßEFµÄĘ½Ćę·Ö±šÓėĄāBB”䔢DD”ä½»ÓŚM”¢N£¬ÉčBM=x£¬x”Ź[0£¬1]£¬øų³öŅŌĻĀĖÄøöĆüĢā£ŗ| 1 | 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| ¦Š |
| 3 |
| 1 |
| 2 |
| 1 |
| f(x) |
| 1 |
| 2 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com