
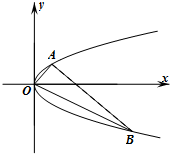
 已知抛物线y2=2px(p>0)上点T(3,t)到焦点F的距离为4.
已知抛物线y2=2px(p>0)上点T(3,t)到焦点F的距离为4.| OA |
| OB |
| OA |
| OB |
| 1 |
| m2 |
| 5μ2+36μ+52 |
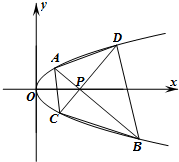 (Ⅰ)解:由已知得3+
(Ⅰ)解:由已知得3+| p |
| 2 |
| 3 |
| ||
| 4 |
| ||
| 4 |
|
| OA |
| OB |
| (y1y2)2 |
| 16 |
| 1+m2 |
| 1+m2 |
| 16m2+80 |
1+(-
|
1+
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1+m2 |
| 16m2+80 |
1+
|
|
(2+(m2+
|
| 1 |
| m2 |
| 5μ2+36μ+52 |


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
| A、方程f(x)=0有实数根?函数y=f(x)有零点 |
| B、函数y=-x2+3x+5有两个零点 |
| C、单调函数至多有一个零点 |
| D、函数f(x)在区间[a,b]上满足f(a)•f(b)<0,则函数f(x)在区间(a,b)内有零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:
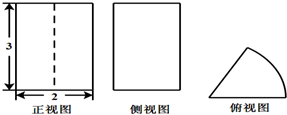 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )A、12+
| ||
B、6+
| ||
| C、12+2π | ||
| D、6+4π |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 2 |
|
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com