
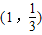 是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足
是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足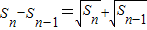 (n≥2).
(n≥2). 的前n项和为Tn,问满足Tn
的前n项和为Tn,问满足Tn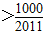 的最小整数是多少?
的最小整数是多少? ,求数列Cn的前n项和Pn.
,求数列Cn的前n项和Pn. 求出{an}的通项公式;根据
求出{an}的通项公式;根据 求出
求出 的通项公式,进而求出Sn,bn的通项公式.
的通项公式,进而求出Sn,bn的通项公式.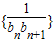 的前n项和为Tn进而解出n.
的前n项和为Tn进而解出n. 是函数f(x)=ax(a>0且a≠1)的图象上一点
是函数f(x)=ax(a>0且a≠1)的图象上一点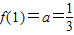
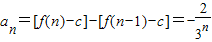
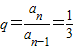
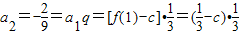
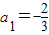 ,
, (3分)
(3分)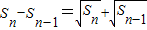 (n≥2)
(n≥2)

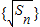 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.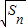 =n,Sn=n2 bn=Sn-Sn-1=n2-(n-1)2=2n-1
=n,Sn=n2 bn=Sn-Sn-1=n2-(n-1)2=2n-1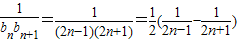
 =
=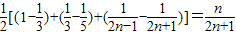
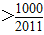 ,
,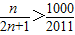 ,即
,即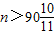
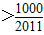 的最小整数为91(11分)
的最小整数为91(11分)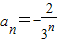 ,bn=2n-1
,bn=2n-1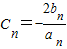 =(2n-1)•3nPn=1•3+3•32+5•33++(2n-1)•3n①
=(2n-1)•3nPn=1•3+3•32+5•33++(2n-1)•3n① (2n-1)•3n+1=(2-2n)•3n+1-6
(2n-1)•3n+1=(2-2n)•3n+1-6

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2012-2013学年甘肃省武威一中高三(上)第一次月考数学试卷(理科)(解析版) 题型:选择题
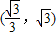 在幂函数f(x)的图象上,则f(x)是( )
在幂函数f(x)的图象上,则f(x)是( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省武威一中高三(上)第一次月考数学试卷(理科)(解析版) 题型:选择题
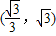 在幂函数f(x)的图象上,则f(x)是( )
在幂函数f(x)的图象上,则f(x)是( )查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省鄂州市高一(下)期末数学试卷(文理合卷)(解析版) 题型:解答题
 是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足
是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足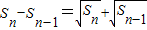 (n≥2).
(n≥2).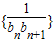 的前n项和为Tn,问满足Tn
的前n项和为Tn,问满足Tn 的最小整数是多少?
的最小整数是多少? ,求数列Cn的前n项和Pn.
,求数列Cn的前n项和Pn.查看答案和解析>>
科目:高中数学 来源:2010-2011学年吉林省长春外国语学校高二(上)期末数学试卷(解析版) 题型:解答题
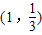 是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足
是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足 (n≥2).
(n≥2).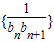 的前n项和为Tn,问满足Tn
的前n项和为Tn,问满足Tn 的最小整数是多少?
的最小整数是多少?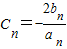 ,求数列Cn的前n项和Pn.
,求数列Cn的前n项和Pn.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com