【题目】已知双曲线
：
经过点
，且其中一焦点
到一条渐近线的距离为1.
（1）求双曲线的方程；
（2）过点
作两条相互垂直的直线
，
分别交双曲线于
，
两点，求点到直线
距离的最大值.
冲刺100分1号卷系列答案
期末好成绩系列答案科目：高中数学 来源： 题型：
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动，为了解小朋友坚持打卡的情况，对该幼儿园所有小朋友进行了调查，调查结果如下表：
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
（1）根据上表数据，求该幼儿园男生平均打卡的天数；
（2）若从打卡21天的小朋友中任选2人交流心得，求选到男生和女生各1人的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线
：
的左、右焦点分别是
、
，左、右两顶点分别是
、
，弦AB和CD所在直线分别平行于x轴与y轴，线段BA的延长线与线段CD相交于点
如图)．
⑴若
是的一条渐近线的一个方向向量，试求的两渐近线的夹角
；
⑵若
，
，
，
，试求双曲线的方程；
⑶在⑴的条件下，且
，点C与双曲线的顶点不重合，直线
和直线
与直线l：
分别相交于点M和N，试问：以线段MN为直径的圆是否恒经过定点？若是，请求出定点的坐标；若不是，试说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂预购软件服务，有如下两种方案：
方案一：软件服务公司每日收取工厂60元，对于提供的软件服务每次10元；
方案二：软件服务公司每日收取工厂200元，若每日软件服务不超过15次，不另外收费，若超过15次，超过部分的软件服务每次收费标准为20元.
（1）设日收费为
元，每天软件服务的次数为
，试写出两种方案中与的函数关系式；
（2）该工厂对过去100天的软件服务的次数进行了统计，得到如图所示的条形图，依据该统计数据，把频率视为概率，从节约成本的角度考虑，从两个方案中选择一个，哪个方案更合适？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，圆锥的顶点为A，底面的圆心为O，BC是底面圆的一条直径，点D，E在底面圆上，已知
，
.
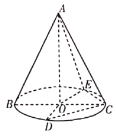
（1）证明：
；
（2）若二面角
的大小为
，求直线OC与平面ACE所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的两焦点分别为
，
，
是椭圆在第一象限内的一点，并满足
，过作倾斜角互补的两直线
、
分别交椭圆于
、
两点.
（1）求点坐标；
（2）当直线经过点
时，求直线
的方程；
（3）求证直线的斜率为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.
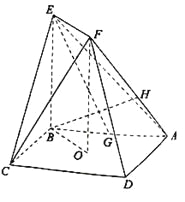
（Ⅰ）求证：EG∥平面ADF；
（Ⅱ）求二面角OEFC的正弦值；
（Ⅲ）设H为线段AF上的点，且AH=
HF，求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
，点F为抛物线的焦点，焦点F到直线3x-4y+3=0的距离为d1，焦点F到抛物线C的准线的距离为d2，且
。
(1)抛物线C的标准方程;
(2)若在x轴上存在点M，过点M的直线l分别与抛物线C相交于P、Q两点，且
为定值，求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
