
ЁОЬтФПЁПКгББЪЁИпПМИФИяКѓИпжабЇЩњЪЕЪЉбЁПЮзпАржЦ,ШєФГаЃбЇЩњбЁдёЮяРэбЇПЦЕФШЫЪ§ЮЊ800ШЫ,ИпЖўЦкжаВтЪдКѓ,гЩбЇЩњЕФЮяРэГЩМЈ,ЕїбабЁПЮзпАржЦбЇЩњЕФбЇЯАЧщПіМАаЇЙћ,ЮЊДЫОіЖЈДгет800ШЫжаГщШЁ![]() ШЫ,ЦфЦЕТЪЗжВМЧщПіШчЯТ:
ШЫ,ЦфЦЕТЪЗжВМЧщПіШчЯТ:
ЗжЪ§ | ЦЕЪ§ | ЦЕТЪ |
| 8 | 0.08 |
| 18 | 0.18 |
| 20 | 0.2 |
|
| 0.24 |
| 15 |
|
| 10 | 0.10 |
| 5 | 0.05 |
КЯМЦ |
| 1 |
(1)МЦЫуБэИёжа![]() ,
,![]() ,
,![]() ЕФжЕ;
ЕФжЕ;
(2)ЮЊСЫСЫНтГЩМЈдк![]() ,
,![]() ЗжЪ§ЖЮбЇЩњЕФЧщПі,ЯШОіЖЈРћгУЗжВуГщбљЕФЗНЗЈДгетСНИіЗжЪ§ЖЮжаГщШЁ6ШЫ,дйДгет6ШЫжаЫцЛњГщШЁ2ШЫНјааУцЬИ,Чѓ2ШЫРДздВЛЭЌЗжЪ§ЖЮЕФИХТЪ.
ЗжЪ§ЖЮбЇЩњЕФЧщПі,ЯШОіЖЈРћгУЗжВуГщбљЕФЗНЗЈДгетСНИіЗжЪ§ЖЮжаГщШЁ6ШЫ,дйДгет6ШЫжаЫцЛњГщШЁ2ШЫНјааУцЬИ,Чѓ2ШЫРДздВЛЭЌЗжЪ§ЖЮЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ,
,![]() ,
,![]() .ЃЈ2ЃЉ
.ЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦЕТЪЕФЖЈвхЃЌЧѓГі![]() ЃЌдйИљОн
ЃЌдйИљОн![]() ЗжЪ§ЖЮЕФЦЕТЪЕУЕН
ЗжЪ§ЖЮЕФЦЕТЪЕУЕН![]() ЃЌИљОн
ЃЌИљОн![]() ЗжЪ§ЖЮЕФЦЕЪ§ЕУЕН
ЗжЪ§ЖЮЕФЦЕЪ§ЕУЕН![]() ЃЛЃЈ2ЃЉИљОн
ЃЛЃЈ2ЃЉИљОн![]() ЃЌ
ЃЌ![]() ЗжЪ§ЖЮбЇЩњЕФШЫЪ§ЃЌРћгУЗжВуГщбљЃЌЕУЕНЫљГщШЁЕФШЫЪ§ЃЌСаГіДгЦфжаГщШЁ
ЗжЪ§ЖЮбЇЩњЕФШЫЪ§ЃЌРћгУЗжВуГщбљЃЌЕУЕНЫљГщШЁЕФШЫЪ§ЃЌСаГіДгЦфжаГщШЁ![]() ШЫЕФЧщПіЃЌИљОнЙХЕфИХаЭЕФИХТЪЙЋЪНЃЌЕУЕНД№АИ.
ШЫЕФЧщПіЃЌИљОнЙХЕфИХаЭЕФИХТЪЙЋЪНЃЌЕУЕНД№АИ.
Нт:(1)вђЮЊ![]() ЗжЪ§ЖЮЕФЦЕЪ§ЮЊ
ЗжЪ§ЖЮЕФЦЕЪ§ЮЊ![]() ЃЌЦЕТЪЮЊ
ЃЌЦЕТЪЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
![]() ЗжЪ§ЖЮЕФЦЕТЪЮЊ
ЗжЪ§ЖЮЕФЦЕТЪЮЊ![]()
Ыљвд![]() ЃЌ
ЃЌ
![]() ЗжЪ§ЖЮЕФЦЕЪ§ЮЊ
ЗжЪ§ЖЮЕФЦЕЪ§ЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() .
.
(2)![]() ЃЌ
ЃЌ![]() ЗжЪ§ЖЮбЇЩњЕФЗжБ№ЮЊ20ШЫЃЌ10ШЫЃЌ
ЗжЪ§ЖЮбЇЩњЕФЗжБ№ЮЊ20ШЫЃЌ10ШЫЃЌ
гУЗжВуГщбљЕФЗНЗЈГщШЁ6ШЫЃЌ
дђ![]() ЗжЪ§ЖЮГщШЁбЇЩњЮЊ4ШЫЃЌМЧЮЊ
ЗжЪ§ЖЮГщШЁбЇЩњЮЊ4ШЫЃЌМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
![]() ЗжЪ§ЖЮГщШЁбЇЩњЮЊ2ШЫЃЌМЧЮЊ
ЗжЪ§ЖЮГщШЁбЇЩњЮЊ2ШЫЃЌМЧЮЊ![]() ЃЌ
ЃЌ![]() .
.
Дгет6ШЫжаЫцЛњГщШЁ2ШЫЃЌЫљгаПЩФмЕФНсЙћЙВга15жжЃЌ
ЫќУЧЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
гжвђЮЊЫљГщШЁ2ШЫРДздВЛЭЌЗжЪ§ЖЮЕФНсЙћга8жжЃЌ
МД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙЪЫљЧѓЕФИХТЪЮЊ![]() .
.


 РјдХЪщвЕЪюМйЯЮНгФўВЈГіАцЩчЯЕСаД№АИ
РјдХЪщвЕЪюМйЯЮНгФўВЈГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() ЃЌдкдВ
ЃЌдкдВ![]() ЃК
ЃК![]() ЩЯШЮШЁвЛЕу
ЩЯШЮШЁвЛЕу![]() ЃЌ
ЃЌ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() .ЃЈШчЭМЃЉ.
.ЃЈШчЭМЃЉ.

ЃЈ1ЃЉЧѓЕу![]() ЕФЙьМЃЗНГЬ
ЕФЙьМЃЗНГЬ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЙ§Еу![]() ЕФЖЏжБЯп
ЕФЖЏжБЯп![]() гыЃЈ1ЃЉжаЕФЙьМЃ
гыЃЈ1ЃЉжаЕФЙьМЃ![]() ЯрНЛгк
ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕу.ЮЪЃКЦНУцФкЪЧЗёДцдквьгкЕу
СНЕу.ЮЪЃКЦНУцФкЪЧЗёДцдквьгкЕу![]() ЕФЖЈЕу
ЕФЖЈЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ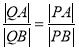 КуГЩСЂЃПЪджЄУїФуЕФНсТл.
КуГЩСЂЃПЪджЄУїФуЕФНсТл.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() .
.
(1)ШєЧњЯп![]() гы
гы![]() дкЫќУЧЕФНЛЕу
дкЫќУЧЕФНЛЕу![]() ДІгаЯрЭЌЕФЧаЯп,ЧѓЪЕЪ§a,bЕФжЕ;
ДІгаЯрЭЌЕФЧаЯп,ЧѓЪЕЪ§a,bЕФжЕ;
(2)ЕБ![]() ЪБ,ШєКЏЪ§
ЪБ,ШєКЏЪ§![]() дкЧјМф
дкЧјМф![]() ФкЧЁгаСНИіСуЕу,ЧѓЪЕЪ§ЕФШЁжЕЗЖЮЇ.
ФкЧЁгаСНИіСуЕу,ЧѓЪЕЪ§ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙ§ХзЮяЯпx2ЃН2py(p>0)ЕФНЙЕуЃЌаБТЪЮЊ![]() ЕФжБЯпНЛХзЮяЯпгкA(x1ЃЌy1)ЃЌB(x2ЃЌy2)(x1<x2)СНЕуЃЌЧв|AB|ЃН9.
ЕФжБЯпНЛХзЮяЯпгкA(x1ЃЌy1)ЃЌB(x2ЃЌy2)(x1<x2)СНЕуЃЌЧв|AB|ЃН9.
(1)ЧѓИУХзЮяЯпЕФЗНГЬЃЛ
(2)OЮЊзјБъдЕуЃЌCЮЊХзЮяЯпЩЯвЛЕуЃЌШє![]() ,ЧѓІЫЕФжЕ.
,ЧѓІЫЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВCЙ§СНЕуAЃЈ0ЃЌ4ЃЉЃЌBЃЈ4ЃЌ6ЃЉЃЌЧвдВаФдкжБЯпxЉ2yЉ2=0ЩЯЃЎ
ЃЈ1ЃЉЧѓдВCЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпlЙ§дЕуЧвБЛдВCНиЕУЕФЯвГЄЮЊ6ЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ,
,![]() .
.
(1)ЬжТлКЏЪ§![]() ЕФЕЅЕїад;
ЕФЕЅЕїад;
(2)ШєВЛЕШЪН![]() дк
дк![]() ЩЯКуГЩСЂ,ЧѓЪЕЪ§
ЩЯКуГЩСЂ,ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЮЊе§ЗНаЮЃЌ
ЮЊе§ЗНаЮЃЌ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЕФжаЕуЃЌвд
ЕФжаЕуЃЌвд![]() ЮЊелКлАб
ЮЊелКлАб![]() елЦ№ЃЌЪЙЕу
елЦ№ЃЌЪЙЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЕФЮЛжУЃЌЧв
ЕФЮЛжУЃЌЧв![]() .
.
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГРКЧђЖгМзЁЂввСНУћдЫЖЏдБСЗЯАЗЃЧђЃЌУПШЫСЗЯА10зщЃЌУПзщЗЃЧђ40ИіЃЎУќжаИіЪ§ЕФОЅвЖЭМШчЭМЃЌдђЯТУцНсТлжаДэЮѓЕФвЛИіЪЧ(ЁЁЁЁ)

A. МзЕФМЋВюЪЧ29 B. МзЕФжаЮЛЪ§ЪЧ24
C. МзЗЃЧђУќжаТЪБШввИп D. ввЕФжкЪ§ЪЧ21
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯп![]() ЩЯЖЏЕу
ЩЯЖЏЕу![]() гыЖЈЕу
гыЖЈЕу![]() ЕФОрРыКЭЫќЕНЖЈжБЯп
ЕФОрРыКЭЫќЕНЖЈжБЯп![]() ЕФОрРыЕФБШЪЧГЃЪ§
ЕФОрРыЕФБШЪЧГЃЪ§![]() ЃЌШєЙ§
ЃЌШєЙ§![]() ЕФЖЏжБЯп
ЕФЖЏжБЯп![]() гыЧњЯп
гыЧњЯп![]() ЯрНЛгк
ЯрНЛгк![]() СНЕу
СНЕу
ЃЈ1ЃЉЫЕУїЧњЯп![]() ЕФаЮзДЃЌВЂаДГіЦфБъзМЗНГЬЃЛ
ЕФаЮзДЃЌВЂаДГіЦфБъзМЗНГЬЃЛ
ЃЈ2ЃЉЪЧЗёДцдкгыЕу![]() ВЛЭЌЕФЖЈЕу
ВЛЭЌЕФЖЈЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() КуГЩСЂЃПШєДцдкЃЌЧѓГіЕу
КуГЩСЂЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com