
【题目】设![]() 是首项为a,公差为d的等差数列(d≠0),
是首项为a,公差为d的等差数列(d≠0), ![]() 是其前n项的和.记
是其前n项的和.记![]() ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.
(1)若c=0,且b1,b2,b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{![]() }是等差数列,证明:c=0.
}是等差数列,证明:c=0.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由c=0,且b1,b2,b4成等比数列,可得d=2a,对于所有的m∈N*,有Sm=m2a,从而对于所有的k,n∈N*,有Snk=(nk)2a=n2k2a=n2Sk;
(2)设数列{bn}的公差为d1,则bn=b1+(n-1)d1,即![]() b1+(n-1)d1,代入
b1+(n-1)d1,代入![]() =na+
=na+![]() d,得
d,得![]() n3+(b1-d1-a+
n3+(b1-d1-a+![]() d)n2+cd1n=c(d1-b1),则对于所有的n∈N*,有An3+Bn2+cd1n=D.(*),在(*)式中分别取n=1,2,3,4,列方程组求解即可.
d)n2+cd1n=c(d1-b1),则对于所有的n∈N*,有An3+Bn2+cd1n=D.(*),在(*)式中分别取n=1,2,3,4,列方程组求解即可.
试题解析:
由题设,Sn=na+![]() d.
d.
(1)由c=0,得bn=![]() =a+
=a+![]() d.
d.
又b1,b2,b4成等比数列,所以b=b1b4,
即![]()
![]() =a
=a![]() ,化简得d2-2ad=0.
,化简得d2-2ad=0.
因为d≠0,所以d=2a.
因此,对于所有的m∈N*,有Sm=m2a.
从而对于所有的k,n∈N*,有Snk=(nk)2a=n2k2a=n2Sk.
(2)设数列{bn}的公差为d1,则bn=b1+(n-1)d1,
即![]() =b1+(n-1)d1,n∈N*,代入Sn的表达式,
=b1+(n-1)d1,n∈N*,代入Sn的表达式,
整理得,对于所有的n∈N*,有
![]() n3+(b1-d1-a+
n3+(b1-d1-a+![]() d)n2+cd1n=c(d1-b1).
d)n2+cd1n=c(d1-b1).
令A=d1-![]() d,B=b1-d1-a+
d,B=b1-d1-a+![]() d,D=c(d1-b1),则对于所有的n∈N*,有An3+Bn2+cd1n=D.(*)
d,D=c(d1-b1),则对于所有的n∈N*,有An3+Bn2+cd1n=D.(*)
在(*)式中分别取n=1,2,3,4,得
A+B+cd1=8A+4B+2cd1=27A+9B+3cd1=64A+16B+4cd1,
从而有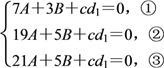
由②,③得A=0,cd1=-5B,代入方程①,得B=0,从而cd1=0.即d1-![]() d=0,b1-d1-a+
d=0,b1-d1-a+![]() d=0,cd1=0.
d=0,cd1=0.
若d1=0,则由d1-![]() d=0,得d=0,与题设矛盾,
d=0,得d=0,与题设矛盾,
所以d1≠0.又cd1=0,所以c=0.


科目:高中数学 来源: 题型:
【题目】[选修4一4:坐标系与参数方程]已知直线l过原点且倾斜角为![]() ,
, ![]()
![]()
![]() ,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为psin
,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为psin![]()
![]() =4cos
=4cos![]() .
.
(I)写出直线l的极坐标方程和曲线C 的直角坐标方程;
(Ⅱ)已知直线l过原点且与直线l相互垂直,若l![]() C=-M,l
C=-M,l![]() C=N,其中M,N不与原点重合,求△OMN 面积的最小值.
C=N,其中M,N不与原点重合,求△OMN 面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域上的任意实数
对其公共定义域上的任意实数![]() 都满足:
都满足: ![]() 和
和![]() 恒成立,则称此直线
恒成立,则称此直线![]() 为
为![]() 和
和![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() ,
, ![]() ,有下列命题:
,有下列命题:
①![]() 在
在![]() 内单调递增;
内单调递增;
②![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的最小值为-4;
的最小值为-4;
③![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的取值范围是
的取值范围是![]() ;
;
④![]() 和
和![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
其中真命题的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一年来,某足球队的![]() 足球运动员每天进行距离球门
足球运动员每天进行距离球门![]() 米远的射门训练
米远的射门训练![]() 次,若打进球门算成功,否则算失败.随机提取该球员连续
次,若打进球门算成功,否则算失败.随机提取该球员连续![]() 天的成功次数统计如下:
天的成功次数统计如下:
![]() .
.
(1)估计该球员一天射门成功次数的四分位数;
(2)若每天![]() 三位球员均进行“三角战术”配合训练,要求三位球员在运动中必须保持如下规则:三人所在的位置构成
三位球员均进行“三角战术”配合训练,要求三位球员在运动中必须保持如下规则:三人所在的位置构成![]() ,
,![]() ,
,![]() 的面积
的面积![]() (平方米).求
(平方米).求![]() 球员之间的距离的最小值(米).
球员之间的距离的最小值(米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足a1=m,an+1=
满足a1=m,an+1=![]() (k∈N*,r∈R),其前n项和为
(k∈N*,r∈R),其前n项和为![]() .
.
(1)当m与r满足什么关系时,对任意的n∈N*,数列{an}都满足an+2=an?
(2)对任意实数m,r,是否存在实数p与q,使得{a2n+1+p}与{a2n+q}是同一个等比数列.若存在,请求出p,q满足的条件;若不存在,请说明理由;
(3)当m=r=1时,若对任意的n∈N*,都有Sn≥λan,求实数λ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 | 频数 | 频率 |
145.5~149.5 | 8 | 0.16 |
149.5~153.5 | 6 | 0.12 |
153.5~157.5 | 14 | 0.28 |
157.5~161.5 | 10 | 0.20 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 |
|
|
合计 |
|
|
(1)求出表中字母![]() 所对应的数值;
所对应的数值;
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5![]() 范围内有多少人?
范围内有多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=3,a2![]() ,且2an+1=3an﹣an-1.
,且2an+1=3an﹣an-1.
(1)求证:数列{an+1﹣an}是等比数列,并求数列{an}通项公式;
(2)求数列{nan}的前n项和为Tn,若![]() 对任意的正整数n恒成立,求k的取值范围.
对任意的正整数n恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com