
分析 (Ⅰ)由椭圆方程可得椭圆长轴长,结合|PF1|=4及椭圆定义可得|PF2|=2,再由勾股定理求得|F1F2|,则c可求,m可求;
(Ⅱ)设出P点坐标,由两点间的距离公式可得关于P点坐标的方程组,则答案可求.
解答 解:(Ⅰ)由已知得:|PF2|=6-4=2,
在△PF1F2中,由勾股定理得,$|{F}_{1}{F}_{2}|=\sqrt{4+16}=\sqrt{20}$,
即4c2=20,解得c2=5.
∴m=9-5=4;
(Ⅱ)设P点坐标为(x0,y0),由(Ⅰ)知,${F}_{1}(-\sqrt{5},0)$,${F}_{2}(\sqrt{5},0)$,
∵$|P{F}_{1}|=\sqrt{({x}_{0}+\sqrt{5})^{2}+{{y}_{0}}^{2}}=4$,$|P{F}_{2}|=\sqrt{({x}_{0}-\sqrt{5})^{2}+{{y}_{0}}^{2}}=2$,
∴$\left\{\begin{array}{l}{({x}_{0}+\sqrt{5})^{2}+{{y}_{0}}^{2}=16}\\{({x}_{0}-\sqrt{5})^{2}+{{y}_{0}}^{2}=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{0}=\frac{3\sqrt{5}}{5}}\\{{y}_{0}=\frac{4\sqrt{5}}{5}}\end{array}\right.$.
∴P($\frac{3\sqrt{5}}{5},\frac{4\sqrt{5}}{5}$).
点评 本题考查椭圆方程的求法,考查了椭圆的简单性质,属中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}π$ | B. | $\frac{2}{3}π$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
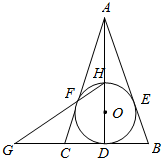 如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.
如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
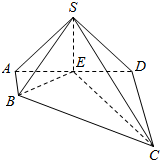 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
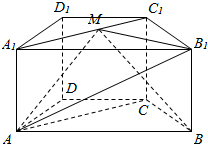 在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.
在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
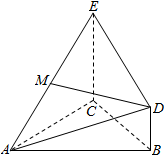 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
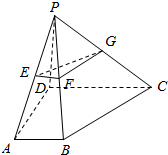 如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.
如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com