
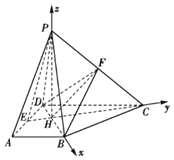
【题目】如图所示,在四棱锥![]() 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,点E为AD的中点,
,点E为AD的中点,![]() ,
,![]() 平面ABCD,且
平面ABCD,且![]()

(1)求证:![]() ;
;
(2)线段PC上是否存在一点F,使二面角![]() 的余弦值是
的余弦值是![]() ?若存在,请找出点F的位置;若不存在,请说明理由.
?若存在,请找出点F的位置;若不存在,请说明理由.
【答案】(1)见证明;(2)见解析
【解析】
(1)由题意,证得![]() ,再由线面垂直的性质,证得
,再由线面垂直的性质,证得![]() ,利用线面垂直的判定定理,即可证得
,利用线面垂直的判定定理,即可证得![]() 平面PEC,进而得到
平面PEC,进而得到![]() .
.
(2)由(1)建立以H为坐标原点,HB、HC、HP所在直线分别为x,y,z轴的坐标系,由![]() 与
与![]() 共线,得
共线,得![]() ,再求得平面CPD和平面CPD的一个法向量,利用向量的夹角公式即可求解.
,再求得平面CPD和平面CPD的一个法向量,利用向量的夹角公式即可求解.
证明:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
E为AD的中点,![]() ,
,
![]() ≌
≌![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,![]() ,
,
又![]() ,且PH,
,且PH,![]() 平面PEC,
平面PEC,![]() 平面PEC,
平面PEC,
又![]() 平面PEC,
平面PEC,![]() .
.
解:(2)由(1)可知![]() ∽
∽![]() ,
,
由题意得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 、EC、BD两两垂直,建立以H为坐标原点,HB、HC、HP所在直线分别为x,y,z轴的坐标系,
、EC、BD两两垂直,建立以H为坐标原点,HB、HC、HP所在直线分别为x,y,z轴的坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
假设线段PC上存在一点F满足题意,
![]() 与
与![]() 共线,
共线,
∴存在唯一实数![]() ,
,![]() ,满足
,满足![]() ,解得
,解得![]() ,
,
设向量![]() 为平面CPD的一个法向量,
为平面CPD的一个法向量,
且![]() ,
,![]() ,
,
∴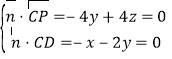 ,取
,取![]() ,得
,得![]() ,
,
同理得平面CPD的一个法向量![]() ,
,
∵二面角![]() 的余弦值是
的余弦值是![]() ,
,
∴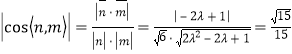 ,
,
由![]() ,解得
,解得![]()


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,03,![]() ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与E交于A、B两点,且
与E交于A、B两点,且![]() ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为![]() ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]()
![]() (
(![]() )的半焦距为
)的半焦距为![]() ,原点
,原点![]() 到经过两点
到经过两点![]() ,
,![]() 的直线的距离为
的直线的距离为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)如图,![]() 是圆
是圆![]()
![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果一个数列从第二项起,后一项与前一项的和相等且为同一常数,这样的数列叫“等和数列”,这个常数叫公和.给出下列命题:
①“等和数列”一定是常数数列;
②如果一个数列既是等差数列又是“等和数列”,则这个数列一定是常数列;
③如果一个数列既是等比数列又是“等和数列”,则这个数列一定是常数列;
④数列![]() 是“等和数列”且公和
是“等和数列”且公和![]() ,则其前
,则其前![]() 项之和
项之和![]() ;
;
其中,正确的命题为__________.(请填出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com