
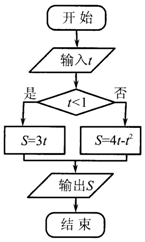
 程序框图如图所示,若输入值t∈(0,3),则输出值S的取值范围是( )
程序框图如图所示,若输入值t∈(0,3),则输出值S的取值范围是( )| A. | (0,4) | B. | (0,4] | C. | [0,9] | D. | (0,3) |
分析 模拟执行程序框图,可得程序框图的功能是计算并输出S=$\left\{\begin{array}{l}{3t}&{t<1}\\{4t-{t}^{2}}&{t≥1}\end{array}\right.$的值,分类讨论即可得解.
解答 解:由程序框图可知程序框图的功能是计算并输出S=$\left\{\begin{array}{l}{3t}&{t<1}\\{4t-{t}^{2}}&{t≥1}\end{array}\right.$的值,
∴当t∈(0,1)时,0≤3t<3;
当t∈[1,3)时,4t-t2=4-(t-2)2∈[3,4],
∴综上得:0≤S≤4.
故选:B.
点评 本题主要考查了程序框图和二次函数的性质,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | 432 | B. | 384 | C. | 308 | D. | 288 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果m⊥n,m⊥α,n∥β,那么α⊥β | |
| B. | 如果m⊥α,n∥α,那么m⊥n | |
| C. | α∥β,m?α,那么m∥β | |
| D. | 如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
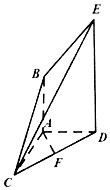 如图,在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AD=AC,AB=$\frac{1}{2}$DE,F是CD的中点.
如图,在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AD=AC,AB=$\frac{1}{2}$DE,F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com