
【题目】已知数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,数列
的等差数列,数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(1)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和;
项和;
(2)若存在正整数![]() ,使得
,使得![]() ,试比较
,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(1)![]() ;(2) 当
;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
审题引导:①等差数列与等比数列对应项的积错位相减求和;②作差比较.
规范解答:解:(1)依题意,a5=b5=b1q5-1=1×34=81,故d=![]() =20,
=20,
所以an=1+20(n-1)=20n-19.(3分)
令Sn=1×1+21×3+41×32+…+(20n-19)·3n-1,①
则3Sn=1×3+21×32+…+(20n-39)·3n-1+(20n-19)·3n,②
①-②,得-2Sn=1+20×(3+32+…+3n-1)-(20n-19)·3n=1+20×![]() -(20n-19)·3n=(29-20n)·3n-29,所以Sn=
-(20n-19)·3n=(29-20n)·3n-29,所以Sn=![]() .(7分)
.(7分)
(2)因为ak=bk,所以1+(k-1)d=qk-1,即d=![]() ,
,
故an=1+(n-1)![]() .又bn=qn-1,(9分)所以bn-an=qn-1-
.又bn=qn-1,(9分)所以bn-an=qn-1-![]()
=![]() [(k-1)(qn-1-1)-(n-1)(qk-1-1)]
[(k-1)(qn-1-1)-(n-1)(qk-1-1)]
=![]() [(k-1)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+q+1)].(11分)
[(k-1)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+q+1)].(11分)
(ⅰ)当1<n<k时,由q>1知
bn-an=![]() [(k-n)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+qn-1)]
[(k-n)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+qn-1)]
<![]() [(k-n)(n-1)qn-2-(n-1)(k-n)qn-1]=-
[(k-n)(n-1)qn-2-(n-1)(k-n)qn-1]=-![]()
<0;(13分)
(ⅱ)当n>k时,由q>1知
bn-an=![]() [(k-1)(qn-2+qn-3+…+qk-1)-(n-k)(qk-2+qk-3+…+q+1)]
[(k-1)(qn-2+qn-3+…+qk-1)-(n-k)(qk-2+qk-3+…+q+1)]
>![]() [(k-1)(n-k)qk-1-(n-k)(k-1)qk-2]
[(k-1)(n-k)qk-1-(n-k)(k-1)qk-2]
=(q-1)2qk-2(n-k)
>0,(15分)
综上所述,当1<n<k时,an<bn;当n>k时,an>bn;当n=1,k时,an=bn.(16分)
(注:仅给出“1<n<k时,an<bn;n>k时,an>bn”得2分)
错因错位相减时项数容易搞错,作差比较后学生不能灵活倒用等比数列求和公式1-qn=(1-q)(1+q+q2+…+qn-1)


科目:高中数学 来源: 题型:
【题目】河道上有一抛物线型拱桥,在正常水位时,拱圈最高点距水面8m,拱圈内水面宽24m,一条船在水面以上部分高6.5m,船顶部宽6m.
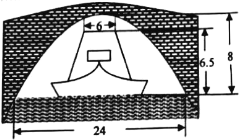
(1)试建立适当的直角坐标系,求拱桥所在的抛物线的标准方程;
(2)近日水位暴涨了1.54m,为此,必须加重船载,降低船身,才能通过桥洞,试问:船身至少应该降低多少?(精确到0.1m)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,上顶点为
,上顶点为![]() ,原点O到直线
,原点O到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆C的标准方程;
(2)若点T在圆![]() 上,点A为椭圆的右顶点,是否存在过点A的直线l交椭圆C于点B(异于点A),使得
上,点A为椭圆的右顶点,是否存在过点A的直线l交椭圆C于点B(异于点A),使得![]() 成立?若存在,求出直线l的方程;若不存在,请说明理由.
成立?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网经济不断发展,网上开店销售农产品的人群越来越多,网上交易额也逐年增加,某一农户农产品连续五年的网银交易额统计表,如下所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网上交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,农户将上表的数据进行了处理,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程.求出![]() 关于
关于![]() 的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
(附:在线性回归方程![]() 中,
中,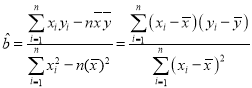 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为![]() ,设圆柱的高度为
,设圆柱的高度为![]() ,底面半径为
,底面半径为![]() ,且
,且![]() ,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为![]() 元
元![]() ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为![]() 元
元![]() 为常数).
为常数).
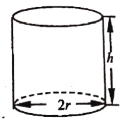
(1)写出易拉罐的制造费用![]() (元)关于
(元)关于![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,∠ABC=30°.△ABD中,∠ADB=90°,∠ABD=45°,且AC=1.将△ABD沿边AB折叠后,

(1)若二面角C—AB—D为直二面角,则直线CD与平面ABC所成角的正切值为_______;
(2)若二面角C—AB—D的大小为150°,则线段CD的长为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,四边形
中,四边形![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 上的动点.
上的动点.
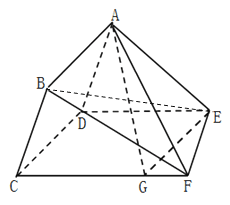
(Ⅰ)当![]() 时,求证
时,求证![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)若二面角![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com