
分析 由2$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,可得-2$\overrightarrow{AP}$+$\overrightarrow{PA}+\overrightarrow{AB}$+$\overrightarrow{PA}+\overrightarrow{AC}$=$\overrightarrow{0}$,化为:$\overrightarrow{AB}$+$\overrightarrow{AC}$=4$\overrightarrow{AP}$,即可得出.
解答 解:∵2$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,
∴-2$\overrightarrow{AP}$+$\overrightarrow{PA}+\overrightarrow{AB}$+$\overrightarrow{PA}+\overrightarrow{AC}$=$\overrightarrow{0}$,化为:$\overrightarrow{AB}$+$\overrightarrow{AC}$=4$\overrightarrow{AP}$,
∵实数λ满足$\overrightarrow{AB}$+$\overrightarrow{AC}$=λ$\overrightarrow{AP}$,则λ=4.
故答案为:4.
点评 本题考查了向量的三角形法则、向量相等,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.
如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
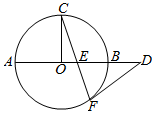 如图,已知AB为⊙O的直径,C、F为⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连结CF交AB于点E.若AB=6,ED=4,则EF=( )
如图,已知AB为⊙O的直径,C、F为⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连结CF交AB于点E.若AB=6,ED=4,则EF=( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\frac{{4\sqrt{5}}}{3}$ | D. | $\frac{{4\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC,以AB为直径的圆O与边BC,AC分别交于点D,E,且DF⊥AC于F.若CD=3,EA=$\frac{7}{5}$,则EF的长为$\frac{9}{5}$.
如图,在△ABC中,AB=AC,以AB为直径的圆O与边BC,AC分别交于点D,E,且DF⊥AC于F.若CD=3,EA=$\frac{7}{5}$,则EF的长为$\frac{9}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ac2>bc2,则a>b | B. | 若a<b<0,则a2<b2 | ||
| C. | 若a>b>0,则$\frac{1}{a}$<$\frac{1}{b}$ | D. | 若a<b<0,c>d>0,则ac<bd |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 甲 | 60 | 80 | 70 | 90 | 70 |
| 乙 | 80 | 60 | 70 | 80 | 75 |
| A. | 甲的平均成绩较好,乙的各门功课发展较平衡 | |
| B. | 甲的平均成绩较好,甲的各门功课发展较平衡 | |
| C. | 乙的平均成绩较好,甲的各门功课发展较平衡 | |
| D. | 乙的平均成绩较好,乙的各门功课发展较平衡 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com