
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)若定义在实数集![]() 上的以2为最小正周期的周期函数
上的以2为最小正周期的周期函数![]() ,当
,当![]() 时,
时,![]() ,试求
,试求![]() 在闭区间
在闭区间![]() 上的表达式,并证明
上的表达式,并证明![]() 在闭区间
在闭区间![]() 上单调递减;
上单调递减;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() (2)
(2)![]() ;证明见解析(3)
;证明见解析(3)![]()
【解析】
(1)根据奇函数与偶函数定义,可分别代入得关于![]() 与
与![]() 的方程组,解方程组即可求得
的方程组,解方程组即可求得![]() 与
与![]() 的解析式;
的解析式;
(2)由![]() 为以2为最小正周期的周期函数,所以当
为以2为最小正周期的周期函数,所以当![]() 时
时![]() ,即可根据
,即可根据![]() 求得求
求得求![]() 在闭区间
在闭区间![]() 上的表达式.根据函数单调性的定义,任取
上的表达式.根据函数单调性的定义,任取![]() ,即可通过作差法证明函数的单调性.
,即可通过作差法证明函数的单调性.
(3)利用换元法,令![]() ,由
,由![]() 可求得
可求得![]() 的取值范围.则
的取值范围.则![]() .由
.由![]() 可知当
可知当![]() 时满足
时满足![]() ,因而可知
,因而可知![]() 恒成立.分离参数
恒成立.分离参数![]() 可知
可知![]() ,结合基本不等式即可求得
,结合基本不等式即可求得![]() 的取值范围.
的取值范围.
(1)由![]() ①,
①,
因为![]() 是偶函数,
是偶函数,![]() 是奇函数
是奇函数
所以有![]() ,即
,即![]() ②
②
∵![]() ,
,![]() 定义在实数集
定义在实数集![]() 上
上
由①和②解得![]() ,
,![]()
(2)![]() 是
是![]() 上以2为正周期的周期函数
上以2为正周期的周期函数
所以当![]() 时,
时,![]()
![]()
![]()
即![]() 在闭区间
在闭区间![]() 上的表达式为
上的表达式为![]()
下面证明![]() 在闭区间
在闭区间![]() 上递减:
上递减:
![]() ,当且仅当
,当且仅当![]()
即![]() 时等号成立.对于任意
时等号成立.对于任意![]()
![]()
![]()
![]()
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
从而![]() ,所以当
,所以当![]() 时,
时,![]() 递减
递减
(3)∵![]() 在
在![]() 单调递增
单调递增
∴![]()
∴![]()
![]() 对于
对于![]() 恒成立
恒成立
∴![]() 对于
对于![]() 恒成立
恒成立
令![]() ,则
,则![]()
当且仅当![]() 时,等号成立,且
时,等号成立,且![]()
所以在区间![]() 上
上![]() 单调递减
单调递减
∴![]()
∴![]() 为
为![]() 的取值范围
的取值范围


科目:高中数学 来源: 题型:
【题目】某市为创建全国文明城市,推出“行人闯红灯系统建设项目”,将针对闯红灯行为进行曝光.交警部门根据某十字路口以往的监测数据,从穿越该路口的行人中随机抽查了![]() 人,得到如图示的列联表:
人,得到如图示的列联表:
闯红灯 | 不闯红灯 | 合计 | |
年龄不超过 |
|
|
|
年龄超过 |
|
|
|
合计 |
|
|
|
(1)能否有![]() 的把握认为闯红灯行为与年龄有关?
的把握认为闯红灯行为与年龄有关?
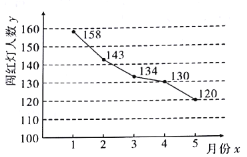
(2)下图是某路口监控设备抓拍的![]() 个月内市民闯红灯人数的统计图.请建立
个月内市民闯红灯人数的统计图.请建立![]() 与
与![]() 的回归方程
的回归方程![]() ,并估计该路口
,并估计该路口![]() 月份闯红灯人数.
月份闯红灯人数.
附: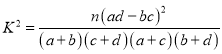
 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海城市的海边有两条相互垂直的直线型公路![]() 、
、![]() ,海岸边界
,海岸边界![]() 近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道
近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段
有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段![]() 是函数
是函数![]() 图像的一段,点M到
图像的一段,点M到![]() 、
、![]() 的距离分别为8千米和1千米,点N到
的距离分别为8千米和1千米,点N到![]() 的距离为10千米,点P到
的距离为10千米,点P到![]() 的距离为2千米.以
的距离为2千米.以![]() 、
、![]() 分别为x,y轴建立如图所示的平面直角坐标系
分别为x,y轴建立如图所示的平面直角坐标系![]() .
.
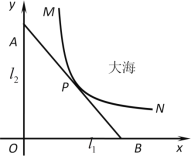
(1)求曲线段![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
(2)求直线![]() 的方程,并求出公路
的方程,并求出公路![]() 的长度(结果精确到1米).
的长度(结果精确到1米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某组委会要从五名志愿者中选派四人分别从事翻译导游礼仪司机四项不同工作,若其中甲不能从事翻译工作,乙不能从事导游工作,其余三人均能从事这四项工作,则不同的选派方案共有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)若定义在实数集![]() 上的以2为最小正周期的周期函数
上的以2为最小正周期的周期函数![]() ,当
,当![]() 时,
时,![]() ,试求
,试求![]() 在闭区间
在闭区间![]() 上的表达式,并证明
上的表达式,并证明![]() 在闭区间
在闭区间![]() 上单调递减;
上单调递减;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,真命题是( )
A.和两条异面直线都相交的两条直线是异面直线
B.和两条异面直线都相交于不同点的两条直线是异面直线
C.和两条异面直线都垂直的直线是异面直线的公垂线
D.若![]() 、
、![]() 是异面直线,
是异面直线,![]() 、
、![]() 是异面直线,则
是异面直线,则![]() 、
、![]() 是异面直线
是异面直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
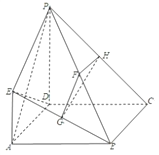
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列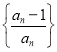 的前
的前![]() 项积,且
项积,且![]() ,求数列
,求数列![]() 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读参考材料,再解决此问题:
参考材料:求抛物线弧![]() (
(![]() )与x轴及直线
)与x轴及直线![]() 所围成的封闭图形的面积
所围成的封闭图形的面积
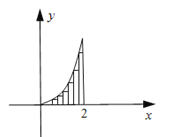
解:把区间![]() 进行n等分,得
进行n等分,得![]() 个分点
个分点![]() (
(![]() ),过分点
),过分点![]() ,作x轴的垂线,交抛物线于
,作x轴的垂线,交抛物线于![]() ,并如图构造
,并如图构造![]() 个矩形,先求出
个矩形,先求出![]() 个矩形的面积和
个矩形的面积和![]() ,再求
,再求![]() ,即是封闭图形的面积,又每个矩形的宽为
,即是封闭图形的面积,又每个矩形的宽为![]() ,第i个矩形的高为
,第i个矩形的高为![]() ,所以第i个矩形的面积为
,所以第i个矩形的面积为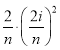 ;
;
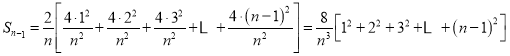
![]()
所以封闭图形的面积为![]()
阅读以上材料,并解决此问题:已知对任意大于4的正整数n,
不等式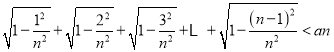 恒成立,
恒成立,
则实数a的取值范围为______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com