
【题目】如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B(其中 ![]() ),那么这一天6时至14时温差的最大值是°C;与图中曲线对应的函数解析式是 .
),那么这一天6时至14时温差的最大值是°C;与图中曲线对应的函数解析式是 . 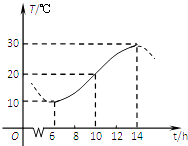
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并证明f(x)的单调性;
(3)求关于x的不等式f(2x﹣1)+f(x+3)>0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 椭圆C1:
椭圆C1: ![]() 表示的是焦点在
表示的是焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 对
对![]() ,直线
,直线![]() 与椭圆C2:
与椭圆C2: ![]() 恒有公共点.
恒有公共点.
(1)若命题“![]() ”是假命题,命题“
”是假命题,命题“![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围.
的取值范围.
(2)若![]() 真
真![]() 假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
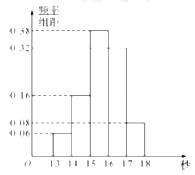
【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
(Ⅰ)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均数(精确到0.1).
(Ⅱ)若从第一、五组中随机取出三名学生成绩,设取自第一组的个数为![]() ,求
,求![]() 的分布列,期望及方差.
的分布列,期望及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(α)= ![]() .
.
(1)若α为第二象限角且f(α)=﹣ ![]() ,求
,求 ![]() 的值;
的值;
(2)若5f(α)=4f(3α+2β).试问tan(2α+β)tan(α+β)是否为定值(其中α≠kπ+ ![]() ,α+β≠kπ+
,α+β≠kπ+ ![]() ,2α+β≠kπ+
,2α+β≠kπ+ ![]() ,3α+2β≠kπ+
,3α+2β≠kπ+ ![]() ,k∈Z)?若是,请求出定值;否则,说明理由.
,k∈Z)?若是,请求出定值;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD﹣A1B1C1D1是正方体,E,F,G,H,M,N分别是所在棱的中点,则下列结论错误的有
①GH和MN是平行直线;GH和EF是相交直线
②GH和MN是平行直线;MN和EF是相交直线
③GH和MN是相交直线;GH和EF是异面直线
④GH和EF是异面直线;MN和EF也是异面直线.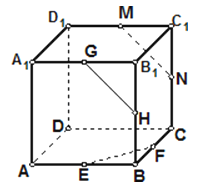
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com