
【题目】如图,在直三棱柱![]() 中,AB=BC,D、E分别为
中,AB=BC,D、E分别为![]() 的中点.
的中点.

(1)证明:ED为异面直线BB1与AC1的公垂线段;
(2)设AB=1, ![]() ,求二面角A1—AD—C1的大小.
,求二面角A1—AD—C1的大小.
【答案】(1)见解析;(2)60°.
【解析】试题分析:(1)设![]() 为
为![]() 中点,连接
中点,连接![]() ,先证明
,先证明![]() 是平行四边形,再证明
是平行四边形,再证明![]() 平面
平面![]() ,从而可得
,从而可得![]() 平面
平面![]() ,可得
,可得![]() 与直线
与直线![]() 与
与![]() 都垂直且相交,进而可得结论;(2)连接
都垂直且相交,进而可得结论;(2)连接![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,根据二面角的平面角定义可知
,根据二面角的平面角定义可知![]() 为二面角
为二面角![]() 的平面角,在直角三角形
的平面角,在直角三角形![]() 中求出正切值即可得结果.
中求出正切值即可得结果.
试题解析:(Ⅰ) 设O为AC中点,连接EO,BO,则EO![]()
![]() C1C,又C1C
C1C,又C1C![]() B1B,所以EO
B1B,所以EO![]() DB,EOBD为平行四边形,ED∥OB.
DB,EOBD为平行四边形,ED∥OB.
∵AB=BC,∴BO⊥AC,
又平面ABC⊥平面ACC1A1,BO面ABC,故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1,BD⊥AC1,ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线.
解:(Ⅱ)连接A1E,由AB=1,AA1=AC=![]() 可知,A1ACC1为正方形,
可知,A1ACC1为正方形,
∴A1E⊥AC1,又由ED⊥平面ACC1A1和ED平面ADC1知平面
ADC1⊥平面A1ACC1,∴A1E⊥平面ADC1.作EF⊥AD,垂足为F,连接A1F,则A1F⊥AD,∠A1FE为二面角A1-AD-C1的平面角.
由已知AB=![]() ED=1, AA1=AC=
ED=1, AA1=AC=![]() ,∴
,∴![]() AE=A1E=1,
AE=A1E=1,
EF=![]() =
=![]() ,
,
tan∠A1FE=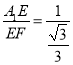 =
=![]() ,∴∠A1FE=60°.
,∴∠A1FE=60°.
所以二面角A1-AD-C1为60°.


科目:高中数学 来源: 题型:
【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取![]() 人看成一个总体,从这
人看成一个总体,从这![]() 人中任意选取
人中任意选取![]() 人,求
人,求![]() 岁以下人数
岁以下人数![]() 的分布列和期望;
的分布列和期望;
(3)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 概率.
概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() R.
R.
(1)证明:当![]() 时,函数
时,函数![]() 是减函数;
是减函数;
(2)根据![]() 的不同取值,讨论函数
的不同取值,讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)当![]() ,且
,且![]() 时,证明:对任意
时,证明:对任意![]() ,存在唯一的
,存在唯一的![]() R,使得
R,使得![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=![]() ,g(x)=x+
,g(x)=x+![]() +a,其中a为常数.
+a,其中a为常数.
(1)若g(x)≥0的解集为{x|0<x![]() 或x≥3},求a的值;
或x≥3},求a的值;
(2)若x1∈(0,+∞),x2∈[1,2]使f(x1)≤g(x2)求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]()
![]() ,过点
,过点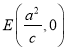 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,且
两点,且![]() ,
,![]() 。
。
(1)求椭圆的离心率;
(2)设点C与点A关于坐标原点对称,直线![]() 上有一点
上有一点![]() 在
在![]()
![]() 的外接圆上,求
的外接圆上,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)某中学高一年级有20个班,每班50人;高二年级有30个班,每班45人.甲就读于高一,乙就读于高二.学校计划从这两个年级中共抽取235人进行视力调查,下列说法中正确的有( )
A.应该采用分层随机抽样法
B.高一、高二年级应分别抽取100人和135人
C.乙被抽到的可能性比甲大
D.该问题中的总体是高一、高二年级的全体学生的视力
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若同时满足下列三个条件:①
,若同时满足下列三个条件:① ![]() ;② 当
;② 当![]() ,且
,且![]() 时,都有
时,都有 ![]() ;③ 当
;③ 当![]() ,且
,且![]() 时,都有
时,都有![]() , 则称
, 则称![]() 为“偏对称函数”.现给出下列三个函数:
为“偏对称函数”.现给出下列三个函数: ![]() ;
; ![]() ;
; ![]() 则其中是“偏对称函数”的函数个数为
则其中是“偏对称函数”的函数个数为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com