Question

4．如图1，在Rt△ABC中，∠ABC=90°，AB=BC=4，点E，F分别在线段AB，AC上，且EF∥BC，将△AEF沿EF折起到△PEF的位置，使得二面角P-EF-B的大小为60°（如图2）．
（1）求证：EF⊥PB；
（2）若点E为AB的中点，求直线PC与平面BCFE所成角的正切值；
（3）求四棱锥P-CBFE体积的最大值．

Answer 1

分析 （1）由EF⊥AB可知折叠后EF⊥PE，EF⊥BE，从而得到EF⊥平面PBE，推出EF⊥PB；
（2）由EF⊥PE，EF⊥BE可知∠PEB即为二面角P-EF-B的平面角，又因为PE=BE，得出△PBE是等边三角形，取BE中点G，连接PG，CG，可证得PG⊥平面BCFE，故∠PCG为直线PC与平面BCFE所成角；
（3）设AE=x则由△AEF∽△ABC可得出EF=x，BE=4-x，过P作平面BCFE的垂线段PH，则PH=$\frac{\sqrt{3}}{2}$x，代入棱锥棱锥体积公式得到关于x的函数，求出该函数的最大值即可．

解答 解：（1）∵折叠前EF⊥AB，∴折叠后EF⊥PE，EF⊥BE，∵PE?平面PBE，BE?平面PBE，PE∩BE=E，
∴EF⊥平面PBE，∵PB?平面PBE，∴EF⊥PB．
（2）取BE中点G，连接PG，CG，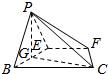
∵EF⊥PE，EF⊥BE，平面PEF∩平面BCFE=EF，PE?PEF，BE?平面BCFE，
∴∠PEB即为二面角P-EF-B的平面角，即∴∠PEB=60°，
∵E为AB的中点，∴PE=BE=$\frac{1}{2}AB=2$，∴△PBE是等边三角形．
∴PG⊥BE，PG=PE•sin60°=$\sqrt{3}$，BG=$\frac{1}{2}$BE=1．
∵EF⊥平面PBE，PG?平面PBE，∴EF⊥PG，
∵BE∩EF=E，BE?平面BCFE，EF?平面BCFE，
∴PG⊥平面BCFE，即∠PCG为直线PC与平面BCFE所成角；
在Rt△BCG中，CG=$\sqrt{B{C}^{2}+B{G}^{2}}$=$\sqrt{17}$．
tan∠PCG=$\frac{PG}{CG}$=$\frac{\sqrt{3}}{\sqrt{17}}$=$\frac{\sqrt{51}}{17}$．
（3）设AE=x，则PE=x，BE=4-x，（0＜x＜4）．
∵∠ABC=90°，AB=BC=4，EF∥BC，
∴EF=AE=x，
过P作PH⊥BE，垂足为H，由（2）可知PH⊥平面BCFE，且PH=PE•sin∠PEB=$\frac{\sqrt{3}}{2}$x，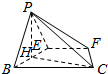
设四棱锥P-CBFE体积位V，则V（x）=$\frac{1}{3}$•S_梯形BCFE•PH=$\frac{1}{3}$•$\frac{1}{2}$•（x+4）（4-x）•$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{12}$（16x-x³）
V′（x）=$\frac{\sqrt{3}}{12}$（16-3x²）．
令V′（x）=$\frac{\sqrt{3}}{12}$（16-3x²）=0得x=$\frac{4\sqrt{3}}{3}$或x=-$\frac{4\sqrt{3}}{3}$（舍）．
当0＜x＜$\frac{4\sqrt{3}}{3}$时，V′（x）＞0，当$\frac{4\sqrt{3}}{3}$＜x＜4时，V′（x）＜0．
∴当x=$\frac{4\sqrt{3}}{3}$时，V（x）取得最大值V（$\frac{4\sqrt{3}}{3}$）=$\frac{\sqrt{3}}{12}$•（16•$\frac{4\sqrt{3}}{3}$-（$\frac{4\sqrt{3}}{3}$）³）=$\frac{32}{9}$．
∴四棱锥P-CBFE体积的最大值是$\frac{32}{9}$．

点评 本题考查了线面垂直的判定与性质，线面角及空间几何体体积计算，找到几何体的高并给出证明是关键．