
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: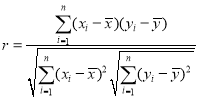 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】(1) ![]() ,
,![]() 与
与![]() 线性相关. (2)见解析,有90%的把握认为购车车主是否购置新能源乘用车与性别有关.(3) 数学期望20.方差12
线性相关. (2)见解析,有90%的把握认为购车车主是否购置新能源乘用车与性别有关.(3) 数学期望20.方差12
【解析】
(1)根据已知数据以及给定公式,求出相关系数,再判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)由调查数据,即可补充列联表,代入![]() 公式,结合附表数据,即可得结论;
公式,结合附表数据,即可得结论;
(3)应用二项分布的期望和方差公式,即可求解.
(1)依题意,
![]() ,
,
![]()
故![]()
![]() ,
,![]() ,
,
则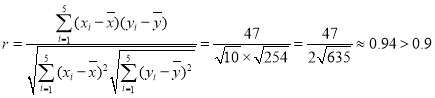
故![]() 与
与![]() 线性相关.
线性相关.
(2)依题意,完善表格如下:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 18 | 6 | 24 |
女性车主 | 2 | 4 | 6 |
总计 | 20 | 10 | 30 |
![]()
故有90%的把握认为购车车主是否购置新能源乘用车与性别有关.
(3)依题意,该地区购置新能源车的车主中女性车主的概率为![]() ,
,
则![]() ,
,
所以![]() ,
,
![]() .
.


科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 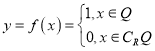 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() ,给出下列四个结论:
,给出下列四个结论:
①曲线C关于原点对称,但不关于x轴、y轴对称;
②曲线C恰好经过4个整点(即横、纵坐标均为整数的点);
③曲线C上任意一点都不在圆![]() 的内部;
的内部;
④曲线C上任意一点到原点的距离都不大于![]() .
.
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地某所高中 2019 年的高考考生人数是 2016 年高考考生人数的 1.5 倍,为了更好地对比该校考生的升学情况,统计了该校 2016 年和 2019年的高考升学情况,得到柱图:
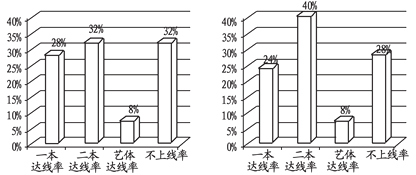
2016年高考数据统计 2019年高考数据统计
则下列结论正确的是( )
A.与2016年相比,2019年一本达线人数有所增加
B.与2016年相比,2019年二本达线人数增加了0.5倍
C.与2016年相比,2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数![]() (
(![]() ,
,![]() ),关于
),关于![]() 的不等式
的不等式![]() 的解集中有且只有一个元素.
的解集中有且只有一个元素.
(1)设数列![]() 的前
的前![]() 项和
项和![]() (
(![]() ),求数列
),求数列![]() 的通项公式;
的通项公式;
(2)设![]() (
(![]() ),则数列
),则数列![]() 中是否存在不同的三项能组成等比数列?请说明理由.
中是否存在不同的三项能组成等比数列?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈[0,1]时,下列关于函数y=![]() 的图象与
的图象与![]() 的图象交点个数说法正确的是( )
的图象交点个数说法正确的是( )
A. 当![]() 时,有两个交点B. 当
时,有两个交点B. 当![]() 时,没有交点
时,没有交点
C. 当![]() 时,有且只有一个交点D. 当
时,有且只有一个交点D. 当![]() 时,有两个交点
时,有两个交点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com