
分析 求出函数的导数,结合二次函数的性质求出a的范围即可.
解答 解:∵f(x)=2x2-ax+lnx,x>0,
∴f′(x)=4x-a+$\frac{1}{x}$=$\frac{{4x}^{2}-ax+1}{x}$,
令g(x)=4x2-ax+1,
若f(x)在其定义域上不单调,
则g(x)在(0,+∞)有解,
∴$\left\{\begin{array}{l}{△{=a}^{2}-16>0}\\{x=\frac{a}{8}>0}\end{array}\right.$,解得:a>4,
则实数a的取值范围是(4,+∞),
故答案为:(4,+∞).
点评 本题考查了函数的单调性问题,考查导数的应用以及二次函数的性质,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 过⊙O外一点P作⊙O的两条割线PAB,PMN,其中PMN过圆心O,过P作再作⊙O的切线PT,切点为T.已知PM=MO=ON=1.
过⊙O外一点P作⊙O的两条割线PAB,PMN,其中PMN过圆心O,过P作再作⊙O的切线PT,切点为T.已知PM=MO=ON=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
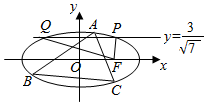 已知右焦点为F的椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>$\sqrt{3}$)与直线y=$\frac{3}{\sqrt{7}}$相交于P,Q两点,且PF⊥QF.
已知右焦点为F的椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>$\sqrt{3}$)与直线y=$\frac{3}{\sqrt{7}}$相交于P,Q两点,且PF⊥QF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com