
”¾ĢāÄæ”æij¹«Ė¾ĪŖׄה¾¼Ć·¢Õ¹µÄĘõ»ś£¬µ÷²éĮĖ½āĮĖ½ü¼øÄź¹ćøęĶ¶Čė¶ŌĻśŹŪŹÕŅęµÄÓ°Ļģ£¬ŌŚČōøÉĻśŹŪµŲĒų·Ö±šĶ¶Čė4ĶņŌŖ¹ćøę·ŃÓĆ£¬²¢½«ø÷µŲµÄĻśŹŪŹÕŅę»ęÖĘ³ÉʵĀŹ·Ö²¼Ö±·½Ķ¼£ØČēĶ¼ĖłŹ¾£©£¬ÓÉÓŚ¹¤×÷ČĖŌ±²Ł×÷Ź§Īó£¬ŗįÖįµÄŹż¾Ż¶ŖŹ§£¬µ«æÉŅŌČ·¶ØŗįÖįŹĒ“Ó0æŖŹ¼¼ĘŹżµÄ.
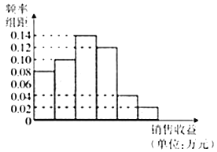
£Ø1£©øł¾ŻĘµĀŹ·Ö²¼Ö±·½Ķ¼¼ĘĖćĶ¼ÖŠø÷Š”³¤·½ŠĪµÄæķ¶Č£»²¢¹Ą¼ĘøĆ¹«Ė¾·Ö±šĶ¶Čė4ĶņŌŖ¹ćøę·ŃÓĆÖ®ŗ󣬶ŌÓ¦µŲĒųĻśŹŪŹÕŅęµÄĘ½¾łÖµ£ØŅŌø÷×éµÄĒų¼äÖŠµćÖµ“ś±ķøĆ×éµÄȔֵ£©£»
£Ø2£©øĆ¹«Ė¾°“ÕÕĄąĖʵÄŃŠ¾æ·½·Ø£¬²āµĆĮķĶāŅ»Š©Źż¾Ż£¬²¢ÕūĄķµĆµ½Čē±ķ£ŗ
¹ćøęĶ¶Čėx£Øµ„Ī»£ŗĶņŌŖ£© | 1 | 2 | 3 | 4 | 5 |
ĻśŹŪŹÕŅęy£Øµ„Ī»£ŗĶņŌŖ£© | 2 | 3 | 2 | 7 |
ÓɱķÖŠµÄŹż¾ŻĻŌŹ¾£¬xÓėyÖ®¼ä“ęŌŚ×ÅĻߊŌĻą¹Ų¹ŲĻµ£¬Ēė½«£Ø1£©µÄ½į¹ūĢīČėæÕ°×Ąø£¬øł¾Ż±ķøńÖŠŹż¾ŻĒó³öy¹ŲÓŚxµÄ»Ų¹éÕęĻß·½³Ģ![]() £¬²¢¹Ą¼ĘøĆ¹«Ė¾ĻĀŅ»ÄźĶ¶Čė¹ćøę·Ń¶ąÉŁĶņŌŖŹ±£¬æÉŹ¹µĆĻśŹŪŹÕŅę“ļµ½8ĶņŌŖ£æ
£¬²¢¹Ą¼ĘøĆ¹«Ė¾ĻĀŅ»ÄźĶ¶Čė¹ćøę·Ń¶ąÉŁĶņŌŖŹ±£¬æÉŹ¹µĆĻśŹŪŹÕŅę“ļµ½8ĶņŌŖ£æ
²Īæ¼¹«Ź½£ŗ×īŠ”¶ž³Ė·Ø¹Ą¼Ę·Ö±šĪŖ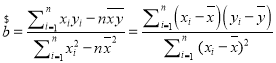 £¬
£¬![]() .
.
”¾“š°ø”æ£Ø1£©æķ¶ČĪŖ£ŗ2£¬ Ę½¾łÖµ£ŗ5£Ø2£©æÕ°×ĄøÖŠĢī5£¬![]() £¬Ķ¶Čė
£¬Ķ¶Čė![]() ĶņŌŖ
ĶņŌŖ
”¾½āĪö”æ
£Ø1£©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ø÷øöŠ”³¤·½ŠĪµÄĆ껿×ÜŗĶĪŖ1£¬½ØĮ¢·½³Ģ£¬¼“æÉĒóµĆ½įĀŪ.ĄūÓĆ×éÖŠÖµ£¬Ēó³ö¶ŌÓ¦ĻśŹŪŹÕŅęµÄĘ½¾łÖµ£»
£Ø2£©ĄūÓĆ¹«Ź½Ēó³ö![]() ¼“æɼĘĖćy¹ŲÓŚxµÄ»Ų¹é·½³Ģ.
¼“æɼĘĖćy¹ŲÓŚxµÄ»Ų¹é·½³Ģ.
£Ø1£©Éč³¤·½ŠĪµÄæķ¶ČĪŖm£¬ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ø÷Š”³¤·½ŠĪĆ껿×ÜŗĶĪŖ1£¬
æÉÖŖ£Ø0.08+0.1+0.14+0.12+0.04+0.02£©m£½1£¬ĖłŅŌm£½2.
Š”×éŅĄ“ĪŹĒ[0£¬2£©£¬[2£¬4£©£¬[4£¬6£©£¬[6£¬8£©£¬[8£¬10£©£¬[10£¬12£©£¬
ĘäÖŠµć·Ö±šĪŖ1£¬3£¬5£¬7£¬9.11
¶ŌÓ¦µÄʵĀŹ·Ö±šĪŖ0.16£¬0.20£¬0.28£¬0.24£¬0.08£¬0.04.
¹ŹæɹĄ¼ĘĘ½¾łÖµĪŖ1”Į0.16+3”Į0.20+5”Į028+7”Į0.24+9”Į0.08+11”Į0.04£½5.
£Ø2£©æÕ°×ĄøÖŠĢī5.
ÓÉĢāŅāæÉÖŖ£¬![]() 3£¬
3£¬![]() 3.8£¬
3.8£¬![]() 69£¬
69£¬![]() 55£¬
55£¬
ĖłŅŌ![]() 1.2£¬
1.2£¬![]() 3.8©1.2”Į3£½0.2.
3.8©1.2”Į3£½0.2.
ĖłŅŌ¹ŲÓŚxµÄ»Ų¹é·½³ĢĪŖ![]()
Č”![]() £¬µĆµ½
£¬µĆµ½![]() .
.


 æŖŠÄĮ·Ļ°æĪæĪĮ·Óėµ„ŌŖ¼ģ²āĻµĮŠ“š°ø
æŖŠÄĮ·Ļ°æĪæĪĮ·Óėµ„ŌŖ¼ģ²āĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() .
.
£Ø¢ń£©ĒóŗÆŹż![]() µÄµ„µ÷Ēų¼ä£»
µÄµ„µ÷Ēų¼ä£»
£Ø¢ņ£©µ±![]() Ź±£¬Čō
Ź±£¬Čō![]() ŌŚ
ŌŚ![]() ÉĻÓŠĮćµć£¬Ē󏵏ż
ÉĻÓŠĮćµć£¬Ē󏵏ż![]() µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚŹżĮŠ![]() £¬Čō“ęŌŚ³£ŹżM£¬Ź¹µĆ¶ŌČĪŅā
£¬Čō“ęŌŚ³£ŹżM£¬Ź¹µĆ¶ŌČĪŅā![]() £¬
£¬![]() Óė
Óė![]() ÖŠÖĮÉŁÓŠŅ»øö²»Š”ÓŚM£¬Ōņ¼Ē×÷
ÖŠÖĮÉŁÓŠŅ»øö²»Š”ÓŚM£¬Ōņ¼Ē×÷![]() £¬ÄĒĆ“ĻĀĮŠĆüĢāÕżČ·µÄŹĒ£Ø £©£®
£¬ÄĒĆ“ĻĀĮŠĆüĢāÕżČ·µÄŹĒ£Ø £©£®
A.Čō![]() £¬ŌņŹżĮŠ
£¬ŌņŹżĮŠ![]() ø÷Ļī¾ł“óÓŚ»ņµČÓŚM£»
ø÷Ļī¾ł“óÓŚ»ņµČÓŚM£»
B.Čō![]() £¬Ōņ
£¬Ōņ![]() £»
£»
C.Čō![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() £»
£»
D.Čō![]() £¬Ōņ
£¬Ōņ![]() £»
£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĖÄĄā׶![]() ÖŠ£¬µ×Ćę
ÖŠ£¬µ×Ćę![]() ŹĒÕż·½ŠĪ£¬¶„µć
ŹĒÕż·½ŠĪ£¬¶„µć![]() ŌŚµ×ĆęµÄÉäÓ°ŹĒµ×ĆęµÄÖŠŠÄ£¬ĒŅø÷¶„µć¶¼ŌŚĶ¬Ņ»ĒņĆęÉĻ£¬ČōøĆĖÄĄā׶µÄ²ąĄā³¤ĪŖ
ŌŚµ×ĆęµÄÉäÓ°ŹĒµ×ĆęµÄÖŠŠÄ£¬ĒŅø÷¶„µć¶¼ŌŚĶ¬Ņ»ĒņĆęÉĻ£¬ČōøĆĖÄĄā׶µÄ²ąĄā³¤ĪŖ![]() £¬Ģå»żĪŖ4£¬ĒŅĖÄĄā׶µÄøßĪŖÕūŹż£¬Ōņ“ĖĒņµÄ°ė¾¶µČÓŚ£Ø £©£Ø²Īæ¼¹«Ź½£ŗ
£¬Ģå»żĪŖ4£¬ĒŅĖÄĄā׶µÄøßĪŖÕūŹż£¬Ōņ“ĖĒņµÄ°ė¾¶µČÓŚ£Ø £©£Ø²Īæ¼¹«Ź½£ŗ![]() £©
£©
A. 2B. ![]() C. 4D.
C. 4D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() .
.
(1)ĒóĒśĻß![]() ŌŚµć
ŌŚµć![]() “¦µÄĒŠĻß·½³Ģ£»
“¦µÄĒŠĻß·½³Ģ£»
(2)Ö¤Ć÷£ŗ![]() ŌŚĒų¼ä
ŌŚĒų¼ä![]() ÉĻÓŠĒŅ½öÓŠ
ÉĻÓŠĒŅ½öÓŠ![]() øöĮćµć.
øöĮćµć.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £¬
£¬![]() £¬
£¬![]() £®
£®
£Ø1£©ĒóŗÆŹż![]() µÄ¼«Öµ£»
µÄ¼«Öµ£»
£Ø2£©Ö±Ļß![]() ĪŖŗÆŹż
ĪŖŗÆŹż![]() Ķ¼ĻóµÄŅ»ĢõĒŠĻߣ¬Čō¶ŌČĪŅāµÄ
Ķ¼ĻóµÄŅ»ĢõĒŠĻߣ¬Čō¶ŌČĪŅāµÄ![]() £¬
£¬![]() ¶¼ÓŠ
¶¼ÓŠ![]() ³ÉĮ¢£¬Ē󏵏ż
³ÉĮ¢£¬Ē󏵏ż![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĶÖŌ²![]() µÄĄėŠÄĀŹĪŖ
µÄĄėŠÄĀŹĪŖ![]() £¬ÓŅ½¹µćĪŖ
£¬ÓŅ½¹µćĪŖ![]() £¬×󶄵ćĪŖA£¬ÓŅ¶„µćBŌŚÖ±Ļß
£¬×󶄵ćĪŖA£¬ÓŅ¶„µćBŌŚÖ±Ļß![]() ÉĻ£®
ÉĻ£®
£Ø¢ń£©ĒóĶÖŌ²CµÄ·½³Ģ£»
£Ø¢ņ£©ÉčµćPŹĒĶÖŌ²CÉĻŅģÓŚA£¬BµÄµć£¬Ö±Ļß![]() ½»Ö±Ļß
½»Ö±Ļß![]() ÓŚµć
ÓŚµć![]() £¬µ±µć
£¬µ±µć![]() ŌĖ¶ÆŹ±£¬ÅŠ¶ĻŅŌ
ŌĖ¶ÆŹ±£¬ÅŠ¶ĻŅŌ![]() ĪŖÖ±¾¶µÄŌ²ÓėÖ±ĻßPFµÄĪ»ÖĆ¹ŲĻµ£¬²¢¼ÓŅŌÖ¤Ć÷£®
ĪŖÖ±¾¶µÄŌ²ÓėÖ±ĻßPFµÄĪ»ÖĆ¹ŲĻµ£¬²¢¼ÓŅŌÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖµćP£Øx£¬y£©ŹĒĘ½ĆęÄŚµÄ¶Æµć£¬¶ØµćF£Ø1£¬0£©£¬¶ØÖ±Ļßl£ŗx=©1ÓėxÖį½»ÓŚµćE£¬¹żµćP×÷PQ”ĶlÓŚµćQ£¬ĒŅĀś×ć![]()
![]()
![]()
![]()
![]() .
.
£Ø1£©Ēó¶ÆµćPµÄ¹ģ¼£tµÄ·½³Ģ£»
£Ø2£©¹żµćF×÷Į½Ģõ»„Ļą“¹Ö±µÄÖ±Ļߣ¬·Ö±š½»ĒśĻßtÓŚµćA,B£¬ŗĶµćC£¬D.ÉčĻ߶ĪABŗĶĻ߶ĪCDµÄÖŠµć·Ö±šĪŖMŗĶN£¬¼ĒĻ߶ĪMNµÄÖŠµćĪŖK£¬µćOĪŖ×ų±źŌµć£¬ĒóÖ±ĻßOKµÄŠ±ĀŹkµÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖÄĄā׶![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() Ę½Ćę
Ę½Ćę![]() £¬µć
£¬µć![]() ŌŚĄā
ŌŚĄā![]() ÉĻ.
ÉĻ.
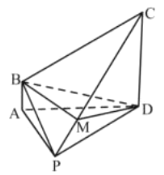
£Ø1£©ĒóÖ¤£ŗĘ½Ćę![]() Ę½Ćę
Ę½Ćę![]() £»
£»
£Ø2£©ČōÖ±Ļß![]() Ę½Ćę
Ę½Ćę![]() £¬Ēó“ĖŹ±ČżĄā×µ
£¬Ēó“ĖŹ±ČżĄā×µ![]() µÄĢå»ż.
µÄĢå»ż.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com