
【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
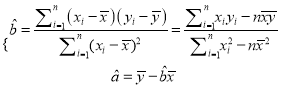
科目:高中数学 来源: 题型:
【题目】某校对高二年段的男生进行体检,现将高二男生的体重![]() 数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组
数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组![]() 的人数为200.根据一般标准,高二男生体重超过
的人数为200.根据一般标准,高二男生体重超过![]() 属于偏胖,低于
属于偏胖,低于![]() 属于偏瘦.观察图形的信息,回答下列问题:
属于偏瘦.观察图形的信息,回答下列问题:
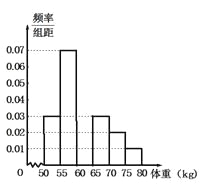
(1)求体重在![]() 内的频率,并补全频率分布直方图;
内的频率,并补全频率分布直方图;
(2)用分层抽样的方法从偏胖的学生中抽取![]() 人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
(3)根据频率分布直方图,估计高二男生的体重的中位数与平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
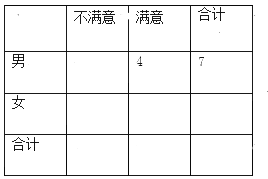
【题目】某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得![]() ,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?

附:

(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程.
已知曲线![]() 的参数方程为
的参数方程为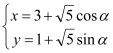 (
(![]() 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线的极坐标方程为![]() ,求直线被曲线
,求直线被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣![]() ﹣(a+2)lnx,其中实数a≥0.
﹣(a+2)lnx,其中实数a≥0.
(1)若a=0,求函数f(x)在x∈[1,3]上的最值;
(2)若a>0,讨论函数f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们用圆的性质类比球的性质如下:
①p:圆心与弦(非直径)中点的连线垂直于弦; q:球心与小圆截面圆心的连线垂直于截面.
②p:与圆心距离相等的两条弦长相等; q:与球心距离相等的两个截面圆的面积相等.
③p:圆的周长为C=πd(d是圆的直径); q:球的表面积为S=πd2(d是球的直径).
④p:圆的面积为S=![]() R·πd(R,d是圆的半径与直径); q:球的体积为V=
R·πd(R,d是圆的半径与直径); q:球的体积为V=![]() R·πd2(R,d是球的半径与直径).
R·πd2(R,d是球的半径与直径).
则上面的四组命题中,其中类比得到的q是真命题的有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com