
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(I)若曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值;
的值;
(II)求函数![]() 的极值;
的极值;
(III)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)当
(2)当![]() 时,函数
时,函数![]() 无极小值;当
无极小值;当![]() ,
, ![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.(3)1
,无极大值.(3)1
【解析】试题分析:(1)求出![]() ,由导数的几何意义,解方程
,由导数的几何意义,解方程![]() 即可;(2)解方程
即可;(2)解方程![]() ,注意分类讨论,以确定
,注意分类讨论,以确定![]() 的符号,从而确定
的符号,从而确定![]() 的单调性,得极大值或极小值(极值点多时,最好列表表示);(3)题意就是方程
的单调性,得极大值或极小值(极值点多时,最好列表表示);(3)题意就是方程![]() 无实数解,即关于
无实数解,即关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解.一般是分类讨论,
上没有实数解.一般是分类讨论, ![]() 时,无实数解,
时,无实数解, ![]() 时,方程变为
时,方程变为![]() ,因此可通过求函数
,因此可通过求函数![]() 的值域来求得
的值域来求得![]() 的范围.
的范围.
试题解析:(1)由![]() ,得
,得![]() .
.
又曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,
轴,
得![]() ,即
,即![]() ,解得
,解得![]() .
.
(2)![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() 为
为![]() 上的增函数,
上的增函数,
所以函数![]() 无极值.
无极值.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
, ![]() .
.
![]() ,
,![]() ;
; ![]() ,
,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极大值.
,无极大值.
综上,当![]() 时,函数
时,函数![]() 无极小值
无极小值
当![]() ,
, ![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
(3)当![]() 时,
时, ![]()
令![]() ,
,
则直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,
没有公共点,
等价于方程![]() 在
在![]() 上没有实数解.
上没有实数解.
假设![]() ,此时
,此时![]() ,
, 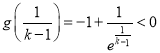 ,
,
又函数![]() 的图象连续不断,由零点存在定理,可知
的图象连续不断,由零点存在定理,可知![]() 在
在![]() 上至少有一解,与“方程
上至少有一解,与“方程![]() 在
在![]() 上没有实数解”矛盾,故
上没有实数解”矛盾,故![]() .
.
又![]() 时,
时, ![]() ,知方程
,知方程![]() 在
在![]() 上没有实数解.
上没有实数解.
所以![]() 的最大值为
的最大值为![]() .
.
解法二:
(1)(2)同解法一.
(3)当![]() 时,
时, ![]() .
.
直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,
没有公共点,
等价于关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,即关于
上没有实数解,即关于![]() 的方程:
的方程:
![]() (*)
(*)
在![]() 上没有实数解.
上没有实数解.
①当![]() 时,方程(*)可化为
时,方程(*)可化为![]() ,在
,在![]() 上没有实数解.
上没有实数解.
②当![]() 时,方程(*)化为
时,方程(*)化为![]() .
.
令![]() ,则有
,则有![]() .
.
令![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
当![]() 时,
时, ![]() ,同时当
,同时当![]() 趋于
趋于![]() 时,
时, ![]() 趋于
趋于![]() ,
,
从而![]() 的取值范围为
的取值范围为![]() .
.
所以当![]() 时,方程(*)无实数解, 解得
时,方程(*)无实数解, 解得![]() 的取值范围是
的取值范围是![]() .
.
综上,得![]() 的最大值为
的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知幂函数y=f(x)的图象过点 ![]() .
.
(1)求函数f(x)的解析式
(2)记g(x)=f(x)+x , 判断g(x)在(1,+∞)上的单调性,并证明之.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 是
是![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于
于![]() 点.
点.

(1)证明:抛物线![]() 在
在![]() 点处的切线与
点处的切线与![]() 平行;
平行;
(2)是否存在实数![]() ,使以
,使以![]() 为直径的圆
为直径的圆![]() 经过
经过![]() 点?若存在,求出
点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x>0时, ![]() .
.
(1)求f(x)的解析式;
(2)讨论函数f(x)的单调性,并求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=ax3﹣x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA , 0)(xA>0); 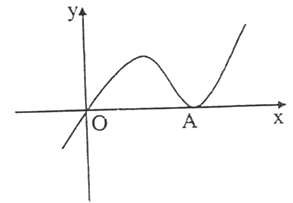
(1)用反证法证明常数c≠0;
(2)如果 ![]() ,求函数的解析式.
,求函数的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在点(1,2)处的切线与f(x)的图象有三个公共点,则b的取值范围是( )
在点(1,2)处的切线与f(x)的图象有三个公共点,则b的取值范围是( )
A.[﹣8,﹣4+2 ![]() )
)
B.(﹣4﹣2 ![]() ,﹣4+2
,﹣4+2 ![]() )
)
C.(﹣4+2 ![]() ,8]
,8]
D.(﹣4﹣2 ![]() ,﹣8]
,﹣8]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乒乓球俱乐部派甲、乙、丙三名运动员参加某运动会的个人单打资格选拔赛,本次选拔赛只有出线和未出线两种情况.若一个运动员出线记![]() 分,未出线记
分,未出线记![]() 分.假设甲、乙、丙出线的概率分别为
分.假设甲、乙、丙出线的概率分别为![]() ,他们出线与未出线是相互独立的.
,他们出线与未出线是相互独立的.
(1)求在这次选拔赛中,这三名运动员至少有一名出线的概率;
(2)记在这次选拔赛中,甲、乙、丙三名运动员所得分之和为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com