
【题目】己知六个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥
;⑥![]() ,从中任选三个函数,则其中既有奇函数又有偶函数的选法共有_______种.
,从中任选三个函数,则其中既有奇函数又有偶函数的选法共有_______种.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
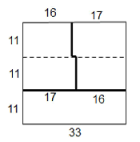
A.33B.56C.64D.78
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果存在实常数a和b,使得函数![]() 总满足
总满足![]() ,我们称这样的函数
,我们称这样的函数![]() 是“
是“![]() 型函数”.请解答以下问题:
型函数”.请解答以下问题:
(1)已知函数![]() 是“
是“![]() 型函数”,求p和b的值;
型函数”,求p和b的值;
(2)已知函数![]() 是“
是“![]() 型函数”,求一组满足条件的k、m和a的值,并说明理由.
型函数”,求一组满足条件的k、m和a的值,并说明理由.
(3)已知函数![]() 是一个“
是一个“![]() 型函数”,且
型函数”,且![]() ,
,![]() 是增函数,若
是增函数,若![]() 是
是![]() 在区间
在区间![]() 上的图像上的点,求点M随着
上的图像上的点,求点M随着![]() 变化可能到达的区域的面积的大小,并证明你的结论.
变化可能到达的区域的面积的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.

(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某高中学生的体能测试结果中,随机抽取100名学生的测试结果,按体重分组得到如图所示的频率分布直方图.
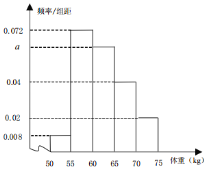
(1)若该校约有![]() 的学生体重不超过“标准体重
的学生体重不超过“标准体重![]() ”,试估计
”,试估计![]() 的值,并说明理由;
的值,并说明理由;
(2)从第3、4、5组中用分层抽样的方法抽取6名学生进行了第二次测试,现从这6人中随机抽取2人进行日常运动习惯的问卷调查,求抽到4组的人数![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com