
【题目】已知a∈R,函数f(x)=ln(x+a)﹣x,曲线y=f(x)与x轴相切. (Ⅰ)求f(x)的单调区间;
(Ⅱ)是否存在实数m使得 ![]() 恒成立?若存在,求实数m的值;若不存在,说明理由.
恒成立?若存在,求实数m的值;若不存在,说明理由.
【答案】解:(Ⅰ)设切点为(x0 , 0),则f′(x)= ![]() , 依题意
, 依题意  ,即
,即  ,
,
解得  .
.
∴f(x)=ln(x+1)﹣x,f′(x)= ![]() .
.
当x变化时,f′(x)与f(x)的变化情况如下表:
x | (﹣1,0) | 0 | (0,+∞) |
f′(x) | + | 0 | ﹣ |
f(x) | 单调递增 | 极大值 | 单调递减 |
∴f(x)在(﹣1,0)上单调递增,在(0,+∞)上单调递减;
(Ⅱ)存在m= ![]() ,理由如下:
,理由如下:![]() 等价于
等价于  ,或
,或  .
.
令g(x)=f(x)﹣mx(1﹣ex)=ln(x+1)﹣x﹣mx(1﹣ex),x∈(﹣1,+∞),
则g′(x)= ![]() ,g″(x)=
,g″(x)= ![]() ,
,
① 若m= ![]() ,
,
当﹣1<x<0时,﹣ ![]() <﹣1,m(x+2)ex<1,∴g″(x)<0;
<﹣1,m(x+2)ex<1,∴g″(x)<0;
当x>0时,﹣ ![]() >﹣1,m(x+2)ex>1,∴g″(x)>0,
>﹣1,m(x+2)ex>1,∴g″(x)>0,
∴g′(x)在单调递减区间为(﹣1,0),单调递增为(0,+∞),
又g′(0)=0,∴g′(x)≥0,当且仅当x=0时,g′(x)=0,
从而g(x)在(﹣1,+∞)上单调递增,又g(0)=0,
∴ ![]() 或
或 ![]() ,即
,即 ![]() >m(1﹣ex)成立.
>m(1﹣ex)成立.
②若m ![]() ,∵g″(0)=2m﹣1>0,
,∵g″(0)=2m﹣1>0,
g″( ![]() )=
)= ![]() <﹣4m2+m(
<﹣4m2+m( ![]() )<0,
)<0,
∴存在x1∈( ![]() ,0),使得g″(x1)=0,
,0),使得g″(x1)=0,
∵g″(x)在(﹣1,0)上单调递增,
∴当x∈(x1 , 0)时,g″(x)>0,g′(x)在(x1 , 0)上递增,
又g′(0)=0,∴当x∈(x1 , 0)时,g′(x)<0,
从而g(x)在(x1 , 0)上递减,又g(0)=0,
∴当x∈(x1 , 0)时,g(x)>0,
此时 ![]() >m(1﹣ex)不恒成立;
>m(1﹣ex)不恒成立;
③若m< ![]() ,同理可得
,同理可得 ![]() >m(1﹣ex)不恒成立.
>m(1﹣ex)不恒成立.
综上所述,存在实数m= ![]()
【解析】(Ⅰ)设出切点坐标,由 ![]() 即可求得a值,把a值代入函数解析式,得到当x变化时,f′(x)与f(x)的变化情况表,由图表可得f(x)的单调区间;(Ⅱ)
即可求得a值,把a值代入函数解析式,得到当x变化时,f′(x)与f(x)的变化情况表,由图表可得f(x)的单调区间;(Ⅱ) ![]() 等价于
等价于 ![]() ,或
,或 ![]() ,令g(x)=f(x)﹣mx(1﹣ex)=ln(x+1)﹣x﹣mx(1﹣ex),x∈(﹣1,+∞),求其二阶导数,然后对m分类讨论得答案.
,令g(x)=f(x)﹣mx(1﹣ex)=ln(x+1)﹣x﹣mx(1﹣ex),x∈(﹣1,+∞),求其二阶导数,然后对m分类讨论得答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() +lnx,a∈R. (Ⅰ)若f(x)在x=1处取得极值,求a的值;
+lnx,a∈R. (Ⅰ)若f(x)在x=1处取得极值,求a的值;
(Ⅱ)若f(x)在区间(1,2)上单调递增,求a的取值范围;
(Ⅲ)讨论函数g(x)=f'(x)﹣x的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人. 
(1)请补充完整频率分布直方图,并估计这组数据的平均数M;
(2)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为x,y.若|x﹣y|≥10,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率P1;
(3)以此样本的频率当作概率,现随机在这组样本中选出3名学生,求成绩不低于120分的人数ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() 在
在![]() 上是单调递增函数,则
上是单调递增函数,则![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】∵![]() ,
,
∴![]() ,
,
又函数![]() 在
在![]() 单调递增,
单调递增,
∴![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立。
上恒成立。
又当![]() 时,
时, ![]() ,
,
∴![]() 。
。
又![]() ,
,
∴![]() 。
。
故实数![]() 的取值范围是
的取值范围是![]() 。
。
答案: ![]()
点睛:对于导函数和函数单调性的关系要分清以下结论:
(1)当![]() 时,若
时,若![]() ,则
,则![]() 在区间D上单调递增(减);
在区间D上单调递增(减);
(2)若函数![]() 在区间D上单调递增(减),则
在区间D上单调递增(减),则![]() 在区间D上恒成立。即解题时可将函数单调性的问题转化为
在区间D上恒成立。即解题时可将函数单调性的问题转化为![]() 的问题,但此时不要忘记等号。
的问题,但此时不要忘记等号。
【题型】填空题
【结束】
19
【题目】某珠宝店丢了一件珍贵珠宝,以下四人中只有一人说真话,只有一人偷了珠宝.甲:我没有偷;乙:丙是小偷;丙:丁是小偷;丁:我没有偷.根据以上条件,可以判断偷珠宝的人是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的极坐标方程为: ![]() .以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线
.以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为:
的参数方程为: 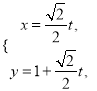 (
(![]() 为参数).
为参数).
(1)求圆C的直角坐标方程和直线l的普通方程;
(2)当θ∈(0,π)时,求直线l与圆C的公共点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. (Ⅰ)求证:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,函数
,函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)是否存在实数![]() 同时满足下列条件:
同时满足下列条件:
①![]() ;
;
②当![]() 的定义域为
的定义域为![]() 时, 值域为
时, 值域为![]() ?若存在, 求出
?若存在, 求出![]() 的值;若不存在, 说明理由.
的值;若不存在, 说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com