
【题目】如图,一张坐标纸上已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.

(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,且直线
两点,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
分析:(1)根据垂直平分线的性质可得![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,且
为焦点的椭圆,且![]() ,可得
,可得![]() ,
,![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ;(2)
;(2)![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 相切,则
相切,则![]() 到
到![]() 的距离:
的距离:![]() ,即
,即![]() , 由
, 由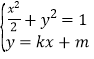 ,消去
,消去![]() ,得
,得![]() ,由平面向量数量积公式可得
,由平面向量数量积公式可得![]() ,由三角形面积公式可得
,由三角形面积公式可得![]() ,换元后,利用单调性可得结果.
,换元后,利用单调性可得结果.
详解:(1)折痕为PP′的垂直平分线,则|MP|=|MP′|,由题意知圆E的半径为![]() ,
,
∴|ME|+|MP|=|ME|+|MP′|=![]() >|EP|,
>|EP|,
∴E的轨迹是以E、P为焦点的椭圆,且![]() ,
,
∴![]() ,∴M的轨迹C的方程为
,∴M的轨迹C的方程为![]() .
.
(2)![]() 与以EP为直径的圆x2+y2=1相切,则O到
与以EP为直径的圆x2+y2=1相切,则O到![]() 的距离:
的距离:
![]() ,即
,即![]() ,
,
由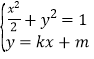 ,消去y,得(1+2k2)x2+4kmx+2m2﹣2=0,
,消去y,得(1+2k2)x2+4kmx+2m2﹣2=0,
∵直线![]() 与椭圆交于两个不同点,
与椭圆交于两个不同点,
∴△=16k2m2﹣8(1+2k2)(m2﹣1)=8k2>0,k2>0,
设A(x1,y1),B(x2,y2),则![]() ,
,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]()
![]()
设μ=k4+k2,则![]() ,∴
,∴![]() ,…10分∵S△AOB关于
,…10分∵S△AOB关于![]() 单调递增,∴
单调递增,∴![]() ,
,
∴△AOB的面积的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
B.当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
C.对任意的实数![]() ,函数
,函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
D.方程![]() 可能有三个实数根.
可能有三个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为P′( ![]() ,
, ![]() );当P是原点时,定义P的“伴随点”为它自身,平面曲线C上所有点的“伴随点”所构成的曲线C′定义为曲线C的“伴随曲线”.现有下列命题:
);当P是原点时,定义P的“伴随点”为它自身,平面曲线C上所有点的“伴随点”所构成的曲线C′定义为曲线C的“伴随曲线”.现有下列命题:
①若点A的“伴随点”是点A′,则点A′的“伴随点”是点A;
②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”C′关于y轴对称;
④一条直线的“伴随曲线”是一条直线.
其中的真命题是(写出所有真命题的序列).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinx+cosωx(ω>0)的图象与x轴交点的横坐标依次构成一个公差为
sinx+cosωx(ω>0)的图象与x轴交点的横坐标依次构成一个公差为 ![]() 的等差数列,把函数f(x)的图象沿x轴向左平移
的等差数列,把函数f(x)的图象沿x轴向左平移 ![]() 个单位,得到函数g(x)的图象,则( )
个单位,得到函数g(x)的图象,则( )
A.g(x)是奇函数
B.g(x)关于直线x=﹣ ![]() 对称
对称
C.g(x)在[ ![]() ,
, ![]() ]上是增函数
]上是增函数
D.当x∈[ ![]() ,
, ![]() ]时,g(x)的值域是[2,1]
]时,g(x)的值域是[2,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 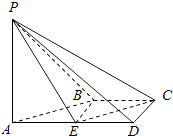
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
:  (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求最后取出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com