[题目]已知P为△ABC内一点.且满足 .记△ABP.△BCP.△ACP的面积依次为S1 . S2 . S3 . 则S1:S2:S3等于( )A.1:2:3B.1:4:9C.2:3:1D.3:1:2 题目和参考答案——青夏教育精英家教网—

【题目】已知P为△ABC内一点，且满足，记△ABP，△BCP，△ACP的面积依次为S1 ， S2 ， S3 ，则S1：S2：S3等于（）
A.1：2：3
B.1：4：9
C.2：3：1
D.3：1：2

【答案】D
【解析】解：如图：设D、E 分别为BC、AC的中点，
∵ =0，∴ ﹣ =﹣3（ + ），
∴ =﹣3×2 =﹣6 ，
同理由（ + ）=﹣2（ + ），即 2 =﹣2× ，
∴ =﹣ ．∴P到BC的距离等于A到BC的距离的，
设△ABC的面积为S，则S2 = S．
P到AC的距离等于B到AC的距离的，
∴S3 = S．∴S1 =S﹣S2﹣S3 = S．
∴S1：S2：S3= S： S= S=3：1：2，
故选D．

根据已知的等式变形可得 =﹣6 ， =﹣ ，从而得出P到BC的距离等于A到BC的距离的，P到AC的距离等于B到AC的距离的．从而有S2 = S，S3 = S，S1 =S﹣S2﹣S3 = S即可解决问题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】（文科）某出租车公司响应国家节能减排的号召，已陆续购买了140辆纯电动汽车作为运营车辆，目前我国主流纯电动汽车按续驶里程数（单位：公里）分为3类，即，， .对这140辆车的行驶总里程进行统计，结果如下表：

（1）从这140辆汽车中任取1辆，求该车行驶总里程超过5万公里的概率；（2）公司为了了解这些车的工作状况，决定抽取14辆车进行车况分析，按表中描述的六种情况进行分层抽样，设从类车中抽取了辆车. （ⅰ）求的值；（ⅱ）如果从这辆车中随机选取2辆车，求恰有1辆车行驶总里程超过5万公里的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题共l2分）

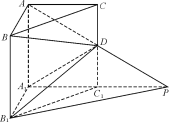
如图，在直三棱柱ABC－A1B1C1中，∠BAC=90°，AB=AC=AA1=1，延长A1C1至点P，使C1P＝A1C1，连接AP交棱CC1于D．

（Ⅰ）求证：PB1∥平面BDA1；

（Ⅱ）求二面角A－A1D－B的平面角的余弦值；

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50]，[50，60]，…，[80，90]，[90，100]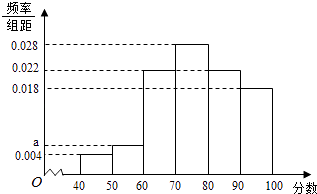

（1）求频率分布图中a的值；
（2）估计该企业的职工对该部门评分不低于80的概率；
（3）从评分在[40，60]的受访职工中，随机抽取2人，求此2人评分都在[40，50]的概率．