
【题目】已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<π),在同一周期内,当 ![]() 时,f(x)取得最大值3;当
时,f(x)取得最大值3;当 ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(1)求函数f(x)的解析式和图象的对称中心;
(2)若 ![]() 时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
【答案】
(1)解:由题意可知A=3,
∵在同一周期内,当 ![]() 时,f(x)取得最大值3;当
时,f(x)取得最大值3;当 ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
∴ ![]() T=
T= ![]()
∴ ![]() ,
,
∴ω=2.
又∵ ![]()
得 ![]() ,
,
∵||<π,
解得 ![]() ,
,
∴函数f(x)的解析式 ![]() .
.
令 ![]() 得
得 ![]()
∴图象的对称中心为 ![]() ,(k∈Z).
,(k∈Z).
(2)解:由(1)知 ![]() .
.
那么:方程2f(x)+1﹣m=0等价于 ![]() 在
在 ![]() 上有且仅有一个实数解
上有且仅有一个实数解
∵ ![]() ,
,
∴ ![]() ,
,
令函数y1=sinu,则u∈ ![]() ,其图象为:
,其图象为:
结合函数图象有, ![]() 或
或 ![]()
解得:m=7或 ![]() .
.
实数m的取值范围为m=7或 ![]() .
.
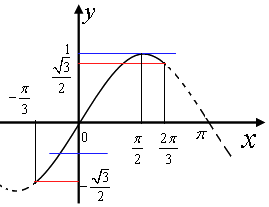
【解析】(1)根据三角函数的性质可得A,当 ![]() 时,f(x)取得最大值3;当
时,f(x)取得最大值3;当 ![]() 时,f(x)取得最小值﹣3.求解周期T,可得ω图象过(
时,f(x)取得最小值﹣3.求解周期T,可得ω图象过( ![]() ,0),带入求解,可得f(x)解析式,令ωx+=kπ,求解对称中心.(2)将f(x)的解析式带入化简,求解
,0),带入求解,可得f(x)解析式,令ωx+=kπ,求解对称中心.(2)将f(x)的解析式带入化简,求解 ![]() 时,画出f(x)的图象,利用数形结合法,可得实数m的取值范围.
时,画出f(x)的图象,利用数形结合法,可得实数m的取值范围.
【考点精析】本题主要考查了正弦函数的对称性的相关知识点,需要掌握正弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() 才能正确解答此题.
才能正确解答此题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2n2+n,n∈N* , 数列{bn}满足an=4log2bn+3,n∈N* .
(1)求an , bn;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[ ![]() ]表示不超过
]表示不超过 ![]() 的最大整数.若 S1=[
的最大整数.若 S1=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=3,
]=3,
S2=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=10,
]=10,
S3=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=21,
]=21,
…,
则Sn=( )
A.n(n+2)
B.n(n+3)
C.(n+1)2﹣1
D.n(2n+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin( ![]() ﹣x)sinx﹣
﹣x)sinx﹣ ![]() cos2x. (I)求f(x)的最小正周期和最大值;
cos2x. (I)求f(x)的最小正周期和最大值;
(II)讨论f(x)在[ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
A.若l⊥m,mα,则l⊥α
B.若l⊥α,l∥m,则m⊥α
C.若l∥α,mα,则l∥m
D.若l∥α,m∥α,则l∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数f(x)的局部对称点.
(1)若a∈R,a≠0,证明:函数f(x)=ax2+x﹣a必有局部对称点;
(2)若函数f(x)=2x+b在区间[﹣1,1]内有局部对称点,求实数b的取值范围;
(3)若函数f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
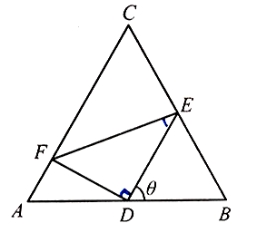
【题目】如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点,![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
(2)求![]() 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com