
【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求:
(1)连续取两次都是红球的概率;
(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数![]() 的概率分布列及期望.
的概率分布列及期望.
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,有一块半椭圆形钢板,其长半轴为![]() ,短半轴为
,短半轴为![]() ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,记
的端点在椭圆上,记![]() ,梯形面积为
,梯形面积为![]() .
.
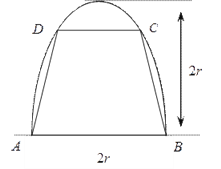
(Ⅰ)求面积![]() 关于变量
关于变量![]() 的函数表达式,并写出定义域;
的函数表达式,并写出定义域;
(Ⅱ)求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确的序号是__________________(写出所有正确命题的序号)
①函数![]() 的图像恒过定点
的图像恒过定点![]() ;
;
②已知集合![]() ,则映射
,则映射![]() 中满足
中满足![]() 的映射共有1个;
的映射共有1个;
③若函数![]() 的值域为R,则实数
的值域为R,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④函数![]() 的图像关于
的图像关于![]() 对称的函数解析式为
对称的函数解析式为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届江苏如东高级中学等四校高三12月联考】已知数列![]() 满足
满足![]() ,
,![]() ,且对任意
,且对任意![]() ,
,![]() 都有
都有![]() .
.
(1)求![]() ,
,![]() ;
;
(2)设![]() (
(![]() ).
).
①求数列![]() 的通项公式;
的通项公式;
②设数列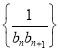 的前
的前![]() 项和
项和![]() ,是否存在正整数
,是否存在正整数![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() ,
,![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|+|x+1|(x∈R).
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象;
(3)写出函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
![]()
表2:女生
![]()
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
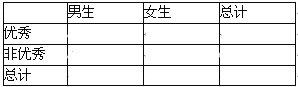
参考数据与公式:
K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0.
(1)求证:f(x)是奇函数;
(2)若f(1)=![]() ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com