Question

把地球看作半径为R的球，A、B是北纬30°圈上的两点，它们的地差为60°，求A、B两点间的球面距离．

Answer 1

【答案】分析：欲求A、B两点间的球面距离，只要求出球心角的大小即可，为此，在三角形ABO中结合题中条件进行求解即得．
解答：解：如图，设30°纬度圈的圆心为O₁，半径为r，
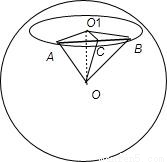
则r=Rcos30°．依题意∠AO₁B=60°，
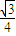
取AB的中点C，则BC=Rcos30°sin30°=R，
在Rt△BOC中，sin∠BOC=sin∠AOB==，
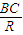
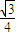
∴∠AOB=2arcsin，
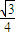
从而A、B两点的球面距离为2Rarcsin．
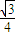
点评：本题主要考查了球的性质，特别是球面距离的求法，涉及到地理知识中的经度纬度的概念．