练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （理）袋中有同样的球个，其中个红色，个黄色，现从中随机且不返回地摸球，每次摸个，当两种颜色的球都被摸到时，即停止摸球，记随机变量为此时已摸球的次数，求：.
    (1)随机变量的概率分布律；
    (2)随机变量的数学期望与方差.
    （理）解：(1)随机变量可取的值为

    得随机变量的概率分布律为：
                
    		2
    		3
    		4




      (2)随机变量的数学期望为：；
    随机变量的方差为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

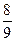    某工厂生产一种精密仪器，产品是否合格需先后经两道相互独立的工序检查，且当第一道工序检查合格后才能进入第二道工序，经长期监测发现，该仪器第一道工序检查合格的概率为，第二道工序检查合格的概率为.已知该厂每月生为3台这种仪器.
    （1）求每生产一台合格仪器的概率；
    （2）用表示每月生产合格仪器的台数，求的分布列和数学期望；
    （3）若生产一台仪器合格可盈利10万元，不合格要亏损3万元，求该厂每月的期望盈利额.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （12分）从四名男生和三名女生中任选3人参加演讲比赛．
    （Ⅰ）求所选3人中至少有一名女生的概率；
    （Ⅱ）表示所选参加演讲比赛的人员中男生的人数，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （满分12分）
    某大学毕业生参加某单位的应聘考试，考核依次分为笔试，面试、实际操作共三轮进行，规定只有通过前一轮考核才能进入下一轮考核，否则被淘汰，三轮考核都通过才能被正式录用，设该大学毕业生通过一、二、三轮考核的概率分别为，且各轮考核通过与否相互独立。
    ①求该大学毕业生进入第三轮考核的概率；
    ②设该大学毕业生在应聘考核中考核轮数为X，求X的概率分布列及期望和方差。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    某单位选派甲、乙、丙三人组队参加“2010上海世博会知识竞赛”，甲、乙、丙三人在同时回答一道问题时，已知甲答对的概率是，甲、丙两人都答错的概率是,乙、丙两人都答对的概率是，规定每队只要有一人答对此题则记该队答对此题.
    （Ⅰ）求该单位代表队答对此题的概率；
    （Ⅱ）此次竞赛规定每队都要回答10道必答题，每道题答对得20分，答错除该题不得分外还要倒扣去10分.若该单位代表队答对每道题的概率相等且回答任一道题的对错对回答其它题没有影响，求该单位代表队必答题得分的期望（精确到1分）.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分10分）
    某省份今年是新课标高考的第一年，某校为了充分了解新课标高考，数学备课组从过去2年的新课标各地模拟卷中挑选出50份试卷进行研究，各地挑选的试卷数如下表所示：
    地区
    		地区A
    		地区B
    		地区C
    		地区D
    试卷数
    		20
    		15
    		5
    		10
      （1）从这50份试卷中随机选出2份，求2份试卷选自同一地区的概率；
    （2）若从C、D两地区挑选出2份试卷进行研究，设挑选出地区C的试卷数为，求随机变量的分布列和数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分12分）下表是某班英语和数学成绩的分布表，已知该班有50名学生，成绩分为1~5个档次。如：表中英语成绩是4分、数学成绩是2分的人数有5人。现设该班任意一位学生的英语成绩为m,数学成绩为n。
    n
    m
    		数学
    5
    		4
    		3
    		2
    		1
     
    英
    语
    		5
    		1
    		3
    		1
    		0
    		1
    4
    		1
    		0
    		7
    		5
    		1
    3
    		2
    		1
    		0
    		9
    		3
    2
    		1
    		b
    		6
    		0
    		a
    1
    		0
    		0
    		1
    		1
    		3
    （1）求m=4,n=3的概率；
    （2）求在m≥3的条件下，n=3的概率；
    （3）求a+b的值，并求m的数学期望；
    （4）若m=2与n=4是相互独立的，求a，b的值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如果是离散型随机变量，，那么（　　）
    A．，B．，
    C．，D．，

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


    （本小题满分10分）2010年3月国家要求一些企业必须停业处理排污问题，于是各企业考虑引进污水处理设备，现有甲、乙两套设备可以引进。每个企业可引进一套，引进两套或都不引进自行研发。对于每个企业，甲被引进的概率为，乙被引进的概率为，甲乙两套设备是否被引进相互独立，各企业之间是否引进也是相互独立的。
    （Ⅰ）求A企业引进污水处理设备的概率；
    （Ⅱ）记X表示3个企业中引进污水处理设备的企业个数，求X的分布列及期望。

    查看答案和解析>>

    同步练习册答案