某同学将命题“在等差数列{an}中,若p+m=2n,则有ap+am=2an(p,m,n∈N*)”改写成:“在等差数列{an}中,若1×p+1×m=2×n,则有1×ap+1×am=2×an(p,m,n∈N*)”,进而猜想:“在等差数列{an}中,若2p+3m=5n,则有2ap+3am=5an(p,m,n∈N*).”
(1)请你判断以上同学的猜想是否正确,并说明理由;
(2)请你提出一个更一般的命题,使得上面这位同学猜想的命题是你所提出命题的特例,并给予证明.
(3)请类比(2)中所提出的命题,对于等比数列{bn},请你写出相应的命题,并给予证明.
【答案】
分析:(1)利用等差数列的通项公式,可把2a
p,3a
m,5a
n都用a
1和d表示,化简即可得到2a
p+3a
m=5a
n(p,m,n∈N
*).
(2)解法一:可以把(1)中具体的数2,3,5用参数s,t,以及s+t代替,就可得到一个更一般的命题,同样用等差数列的通项公式,把数列中的每一项用a
1和d表示,化简即可证明.
解法二:可把(1)中左,右边两项推广到多项相加,只要项的前面系数和相等,就有项之和相等,同样用用等差数列的通项公式,把数列中的每一项用a
1和d表示,化简即可证明.
(3)解法一:类比等差数列的性质,得到等比数列的性质,就是把等差数列中的差变为商,和变为积,n倍变为n次方,即可把(2)中解法一类比过去.证明可以用等比数列的通项公式,把数列中的每一项用a
1和q表示,再化简即可.
解法二:和解法一一样,把(2)中解法二类比过去,用等比数列的通项公式,把数列中的每一项用a
1和q表示,再化简即可.
解答:解:(1)命题“在等差数列{a
n}中,若2p+3m=5n,则有2a
p+3a
m=5a
n(p,m,n∈N
*)”正确.
证明:设等差数列{a
n}的首项为a
1,公差为d,由2p+3m=5n得:2a
p+3a
m=2[a
1+(p-1)d]+3[a
1+(m-1)d]=5a
1+d(2p+3m-5)=5a
1+5(n-1)d=5[a
1+(n-1)d]=5a
n,所以命题成立.
(2)解法一:在等差数列{a
n}中,若sp+tm=kn,s+t=k,则有sa
p+ta
m=ka
n(s,t,k,p,m,n∈N
*).显然,当s=2,t=3,k=5时为以上某同学的猜想.
证明:设等差数列{a
n}的首项为a
1,公差为d,由sp+tm=kn,s+t=k得sa
p+ta
m=s[a
1+(p-1)d]+t[a
1+(m-1)d]=(s+t)a
1+d(sp+tm-s-t)=ka
1+d(kn-k)=k[a
1+(n-1)d]=ka
n,所以命题成立.
(3)解法一:在等比数列{b
n}中,
若sp+tm=kn,s+t=k,则有b
ps•b
mt=b
nk(s,t,k,p,m,n∈N
*).
证明:设等比数列{b
n}的首项为b
1,公比为q,由sp+tm=kn,s+t=k(s,t,k,p,m,n∈N
*)得,b
ps•b
mt=(b
1q
p-1)
s•(b
1q
m-1)
t=b
1s+tq
ps+mt-(s+t)=b
1kq
k(n-1)=(b
1q
n-1)
k=b
nk,所以命题成立.
(2)解法二:在等差数列{a
n}中,若m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t,则有

(m
1,m
2,…,m
s,n
1,n
2,…,n
t,p
1,p
2,…,p
s,q
1,q
2,…,q
t∈N
*).
显然,当s=2,t=1,m
1=2,m
2=3,n
1=5,p=p
1,m=p
2,n=q
1时为某同学的猜想
证明:设等差数列{a
n}的首项为a
1,公差为d,由m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t得

=(m
1+m
2+…+m
s)a
1-(m
1+m
2+…+m
s)d+(m
1p
1+m
2p
2+…+m
sp
s)d
=(n
1+n
2+…+n
t)a
1-(n
1+n
2+…+n
t)d+(n
1q
1+n
2q
2+…+n
tq
t)d
=n
1[a
1+(q
1-1)d]+n
2[a
2+(q
2-1)d]+…+n
s[a
1+(q
s-1)]
=

,所以命题成立.
(3)解法二:在等比数列{b
n}中,若m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t,,则有

(m
1,m
2,…,m
s,n
1,n
2,…,n
t,p
1,p
2,…,p
s,q
1,q
2,…,q
t∈N
*).
证明:设等比数列{b
n}的首项为b
1,公比为q,由m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t得,

=

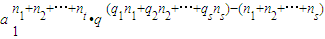
=

=

,所以命题成立.
点评:本题主要考查了应用等差数列,等比数列的通项公式证明等差,等比数列的性质.


 =(m1+m2+…+ms)a1-(m1+m2+…+ms)d+(m1p1+m2p2+…+msps)d
=(m1+m2+…+ms)a1-(m1+m2+…+ms)d+(m1p1+m2p2+…+msps)d ,所以命题成立.
,所以命题成立. 
 =
=
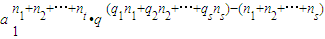
 =
= ,所以命题成立.
,所以命题成立.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案![]() 中,若
中,若![]() ,则有
,则有![]() (
(![]() )”改写成:“在等差数列
)”改写成:“在等差数列![]() 中,若
中,若![]() ,则有
,则有![]() (
(![]() )”,进而猜想:“在等差数列
)”,进而猜想:“在等差数列![]() 中,若
中,若![]() ,则有
,则有![]() (
(![]() ).”
).”![]() ,请你写出相应的命题,并给予证明.
,请你写出相应的命题,并给予证明.![]() 中,若
中,若![]() ,则有
,则有![]() (
(![]() )”改写成:“在等差数列
)”改写成:“在等差数列![]() 中,若
中,若![]() ,则有
,则有![]() (
(![]() )”,进而猜想:“在等差数列
)”,进而猜想:“在等差数列![]() 中,若
中,若![]() ,则有
,则有![]() (
(![]() ).”
).”![]() ,请你写出相应的命题,并给予证明.
,请你写出相应的命题,并给予证明.