
【题目】已知集合A={x|y= ![]() },B={x|x<﹣4或x>2}
},B={x|x<﹣4或x>2}
(1)若m=﹣2,求A∩(RB);
(2)若A∪B=B,求实数m的取值范围.
【答案】
(1)解:m=﹣2,A={x|y= ![]() }={x|x≤﹣1},RB={x|﹣4≤x≤2},
}={x|x≤﹣1},RB={x|﹣4≤x≤2},
∴A∩(RB)={x|﹣4≤x≤﹣1};
(2)解:若A∪B=B,则AB,
∵A={x|x≤1+m},B={x|x<﹣4或x>2}
∴1+m<﹣4,
∴m<﹣5.
【解析】(1)若m=﹣2,A={x|y= ![]() }={x|x≤﹣1},RB={x|﹣4≤x≤2},即可求A∩(RB);(2)若A∪B=B,AB,利用A={x|x≤1+m},B={x|x<﹣4或x>2},即可求实数m的取值范围.
}={x|x≤﹣1},RB={x|﹣4≤x≤2},即可求A∩(RB);(2)若A∪B=B,AB,利用A={x|x≤1+m},B={x|x<﹣4或x>2},即可求实数m的取值范围.
【考点精析】本题主要考查了交、并、补集的混合运算的相关知识点,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的函数,满足f(x)=f(4﹣x),且对任意x1 , x2∈(0,+∞),都有(x1﹣x2)[f(x1+2)﹣f(x2+2)]>0,则满足f(2﹣x)=f( ![]() )的所有x的和为( )
)的所有x的和为( )
A.﹣3
B.﹣5
C.﹣8
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( ) 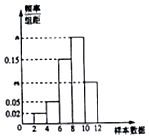
A.0.10
B.0.11
C.0.12
D.0.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴交于点D,且有|FA|=|FD|,当点A的横坐标为3时,△ADF为正三角形
(1)求C的方程
(2)延长AF交抛物线于点E,过点E作抛物线的切线l1 , 求证:l1∥l.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logax(a>0且a≠1)在区间[1,2]上的最大值与函数g(x)=﹣ ![]() 在区间[1,2]上的最大值互为相反数.
在区间[1,2]上的最大值互为相反数.
(1)求a的值;
(2)若函数F(x)=f(x2﹣mx﹣m)在区间(﹣∞,1﹣ ![]() )上是减函数,求实数m的取值范围.
)上是减函数,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<π)图象的最高点D的坐标为 ![]() ,与点D相邻的最低点坐标为
,与点D相邻的最低点坐标为 ![]() . (Ⅰ)求函数f(x)的解析式;
. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)求满足f(x)=1的实数x的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com