
【题目】设等比数列a1,a2,a3,a4的公比为q,等差数列b1,b2,b3,b4的公差为d,且![]() .记
.记![]() (i1,2,3,4).
(i1,2,3,4).
(1)求证:数列![]() 不是等差数列;
不是等差数列;
(2)设![]() ,
, ![]() .若数列
.若数列![]() 是等比数列,求b2关于d的函数关系式及其定义域;
是等比数列,求b2关于d的函数关系式及其定义域;
(3)数列![]() 能否为等比数列?并说明理由.
能否为等比数列?并说明理由.
【答案】(1)证明见解析;(2)答案见解析;(3)答案见解析.
【解析】试题分析:(1)假设数列![]() 是等差数列,则
是等差数列,则![]() ,即
,即![]() ,根据
,根据![]()
![]() 是等差数列及
是等差数列及![]()
![]() 是等比数列,找出矛盾,假设不成立;(2)由
是等比数列,找出矛盾,假设不成立;(2)由![]() ,
, ![]() 得
得![]() ,根据数列
,根据数列![]() 是等比数列得
是等比数列得![]() ,化简求得
,化简求得![]() ,再根据
,再根据![]() ,即可求得
,即可求得![]() 得范围;(3)方法一:设
得范围;(3)方法一:设![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,则
,则 ,解方程组即可;方法二:假设数列
,解方程组即可;方法二:假设数列![]() 是等比数列,则
是等比数列,则![]() ,化简得
,化简得![]() ,即可求得
,即可求得![]() ,与
,与![]() 且
且![]() 矛盾,故可得证.
矛盾,故可得证.
试题解析:(1)假设数列![]() 是等差数列,则
是等差数列,则![]() ,即
,即![]() .
.
∵![]()
![]() 是等差数列
是等差数列
∴![]() ,从而
,从而![]() .
.
又∵![]()
![]() 是等比数列
是等比数列
∴![]() .
.
∴![]() ,这与
,这与![]() 矛盾,从而假设不成立.
矛盾,从而假设不成立.
∴数列![]() 不是等差数列.
不是等差数列.
(2)∵![]() ,
, ![]()
∴![]() .
.
∵![]()
∴![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() .
.
∴![]() 且
且![]() .
.
又∵![]() ,
,
∴![]() ,定义域为
,定义域为![]() .
.
(3)方法一:
设![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,则
,则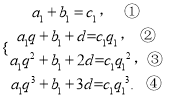
将①+③-2×②得, ![]()
将②+④-2×③得, ![]()
∵![]() ,
, ![]() ,由⑤得
,由⑤得![]() ,
, ![]() .
.
由⑤⑥得![]() ,从而
,从而![]() .
.
代入①得![]() .
.
再代入②,得![]() ,与
,与![]() 矛盾.
矛盾.
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() 不成等比数列.
不成等比数列.
方法二:
假设数列![]() 是等比数列,则
是等比数列,则![]() .
.
∴![]() ,即
,即![]() .
.
两边同时减1得, ![]() .
.
∵等比数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的公比为
的公比为![]()
∴![]() .
.
又∵![]()
∴![]() ,即
,即![]() .这与
.这与![]() 且
且![]() 矛盾.
矛盾.
∴假设不成立.
∴数列![]() 不能为等比数列.
不能为等比数列.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是增函数,则
上是增函数,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
若函数f(x)=log2(x2﹣ax+3a)在[2,+∞)上是增函数,则x2﹣ax+3a>0且f(2)>0,根据二次函数的单调性,我们可得到关于a的不等式,解不等式即可得到a的取值范围.
若函数f(x)=log2(x2﹣ax+3a)在[2,+∞)上是增函数,
则当x∈[2,+∞)时,
x2﹣ax+3a>0且函数f(x)=x2﹣ax+3a为增函数
即![]() ,f(2)=4+a>0
,f(2)=4+a>0
解得﹣4<a≤4
故选:C.
【点睛】
本题考查的知识点是复合函数的单调性,二次函数的性质,对数函数的单调区间,其中根据复合函数的单调性,构造关于a的不等式,是解答本题的关键.
【题型】单选题
【结束】
10
【题目】圆锥的高![]() 和底面半径
和底面半径![]() 之比
之比![]() ,且圆锥的体积
,且圆锥的体积![]() ,则圆锥的表面积为( )
,则圆锥的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(![]() )①前
)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由.②通项公式为
是否是“回归数列”?并请说明理由.②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(![]() )设
)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值.
的值.
(![]() )是否对任意的等差数列
)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() 恰好为线段
恰好为线段![]() 的三等分点,求直线
的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C分别为△ABC的三边a,b,c所对的角,向量![]() =(sin A,sin B),
=(sin A,sin B),![]() =(cos B,cos A),且
=(cos B,cos A),且![]() =sin 2C.
=sin 2C.
(1)求角C的大小;
(2)若sin A,sin C,sin B成等差数列,且![]() ,求边c的长.
,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.

(1)设G,H分别为PB,AC的中点,求证:GH//平面PAD;
(2)求证:![]() ⊥平面PCD;
⊥平面PCD;
(3)求直线AD与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,所有棱长均相等,且AA1⊥平面ABC,点D、E、F分别为所在棱的中点.

(1)求证:EF∥平面CDB1;
(2)求异面直线EF与BC所成角的余弦值;
(3)求二面角B1﹣CD﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·衢州调研)已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P在底面ABCD的射影,N是PC的中点.

(1)求证:平面MPB⊥平面PBC;
(2)若MP=MC,求直线BN与平面PMC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com