
【题目】已知函数![]() 的最大值为
的最大值为![]() .
.
(1)若关于![]() 的方程
的方程![]() 的两个实数根为
的两个实数根为![]() ,求证:
,求证:![]() ;
;
(2)当![]() 时,证明函数
时,证明函数![]() 在函数
在函数![]() 的最小零点
的最小零点![]() 处取得极小值.
处取得极小值.
【答案】(1)见解析;(2)见解析.
【解析】分析:(1)本小问的解决方法是利用![]() 这个条件,得到含有
这个条件,得到含有![]() 的等式,对等式进行变形处理,使得等式左边是
的等式,对等式进行变形处理,使得等式左边是![]() ,右边是分式
,右边是分式![]() 。则求证目标不等式等价于证等式右端的部分
。则求证目标不等式等价于证等式右端的部分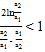 ,运用作差比较法构造函数
,运用作差比较法构造函数![]() ,对
,对![]() 运用导数进行研究,即可证明原不等式;
运用导数进行研究,即可证明原不等式;
(3)讨论函数的单调性,取绝对值得到![]() 的分段形式,若证明
的分段形式,若证明![]() ,则证明
,则证明![]() ,记
,记![]() ,求导分析单调性即可证得.
,求导分析单调性即可证得.
详解:(1)![]() ,由
,由![]() ,
,
得![]() ;由
;由![]() ,得
,得![]() ;
;
所以,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,
所以![]() ,
,
不妨设![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴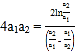 ,
,
设![]() ,则
,则![]() ,
,
所以,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,则
,则![]() ,
,
因![]() ,故
,故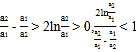 ,所以
,所以![]() ;
;
(2)由(1)可知,![]() 在区间
在区间![]() 单调递增,又
单调递增,又![]() 时,
时,![]() ,
,
易知,![]() 在
在![]() 递增,
递增,![]() ,
,
∴![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
当![]() 时,
时,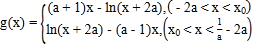 ,
,
于是![]() 时,
时,![]() ,
,
所以,若证明![]() ,则证明
,则证明![]() ,
,
记![]() ,
,
则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 内单调递增,∴
内单调递增,∴![]() ,
,
∵![]() ,
,
∴![]() 在
在![]() 内单调递增,
内单调递增,
∴![]() ,
,
于是![]() 时,
时,![]() .
.
所以![]() 在
在![]() 递减.
递减.
当![]() 时,相应的
时,相应的![]() .
.
所以![]() 在
在![]() 递增.
递增.
故![]() 是
是![]() 的极小值点.
的极小值点.


科目:高中数学 来源: 题型:
【题目】如图是正四面体的平面展开图,![]() 分别是
分别是![]() 的中点,在这个正四面体中:①
的中点,在这个正四面体中:①![]() 与
与![]() 平行;②
平行;②![]() 与
与![]() 为异面直线;③
为异面直线;③![]() 与
与![]() 成60°角;④
成60°角;④![]() 与
与![]() 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,海中一小岛C周围![]() nmile内有暗礁,货轮由西向东航行至A处测得小岛C位于北偏东75°方向上,航行8nmile后,于B处测得小岛C在北偏东60°方向上.
nmile内有暗礁,货轮由西向东航行至A处测得小岛C位于北偏东75°方向上,航行8nmile后,于B处测得小岛C在北偏东60°方向上.

(1)如果这艘货轮不改变航向继续前进,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘货轮在B处改变航向为南偏东α°(α>0)方向航行,顺利绕过暗礁,求a的最大值.(附:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年央视大型文化节目《经典咏流传》的热播,在全民中掀起了诵读诗词的热潮.某大学社团调查了该校文学院300名学生每天诵读诗词的时间(所有学生诵读时间都在两小时内),并按时间(单位:分钟)将学生分成六个组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,经统计得到了如图所
,经统计得到了如图所
示的频率分布直方图
(Ⅰ)求频率分布直方图中![]() 的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;
的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;
(Ⅱ)若两个同学诵读诗词的时间![]() 满足
满足![]() ,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.
,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列4个命题:
(1)“若![]() ,则
,则![]() 互为相反数”的否命题
互为相反数”的否命题
(2)“若![]() ,则
,则![]() ”的逆否命题
”的逆否命题
(3)“若![]() ,则
,则![]() ”的否命题
”的否命题
(4)“若![]() ,则
,则![]() 有实数根”的逆命题
有实数根”的逆命题
其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】

如图,在四面体![]() 中,
中,![]() 点
点![]() 分别是棱
分别是棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:四边形![]() 为矩形;
为矩形;
(Ⅲ)是否存在点![]() ,到四面体
,到四面体![]() 六条棱的中点 的距离相等?说明理由.
六条棱的中点 的距离相等?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com