

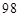 分,(3)0.75.
分,(3)0.75.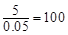 人,又各班被抽取的学生人数成等差数列,人数最少的班被抽取了22人,则首项为22.设公差为d,则
人,又各班被抽取的学生人数成等差数列,人数最少的班被抽取了22人,则首项为22.设公差为d,则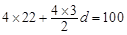 ,
,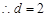 ,因此各班被抽取的人数分别是22人,24人,26人,28人,(2)因为平均成绩为各组中值与对应概率乘积的和,即
,因此各班被抽取的人数分别是22人,24人,26人,28人,(2)因为平均成绩为各组中值与对应概率乘积的和,即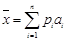 ,由频率分布条形图知,
,由频率分布条形图知,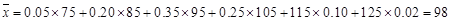 (3)在抽取的所有学生中,任取一名学生,分数不低于90分的概率等于1减去分数低于90分的概率. 而分数低于90分的概率等于
(3)在抽取的所有学生中,任取一名学生,分数不低于90分的概率等于1减去分数低于90分的概率. 而分数低于90分的概率等于 ,因此所求概率为1
,因此所求概率为1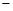 0.25=0.75.
0.25=0.75.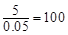 人 2分
人 2分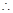 各班被抽取的学生人数成等差数列,设公差为d,则
各班被抽取的学生人数成等差数列,设公差为d,则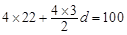
 6分
6分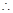 各班被抽取的人数分别是22人,24人,26人,28人 8分
各班被抽取的人数分别是22人,24人,26人,28人 8分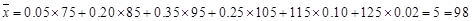 分 11分
分 11分 0.25="0.75." 14分
0.25="0.75." 14分

科目:高中数学 来源:不详 题型:解答题
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |

 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
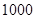 人,其中
人,其中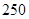 名工人参加过短期培训(称为
名工人参加过短期培训(称为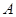 类工人),另外
类工人),另外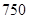 名工人参加过长期培训(称为
名工人参加过长期培训(称为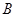 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按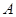 类、
类、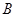 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查  名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).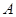 类工人和
类工人和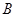 类工人中各抽查多少工人?
类工人中各抽查多少工人?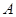 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.| 生产能力分组 | 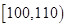 | 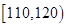 | 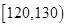 | 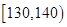 | 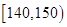 |
| 人数 | 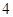 | 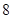 | 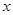 | 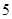 | 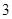 |
| 生产能力分组 | 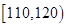 | 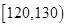 | 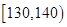 | 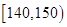 |
| 人数 | 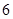 | 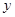 | 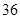 | 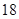 |
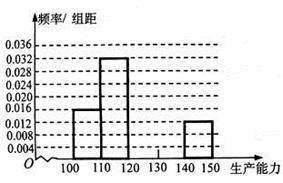
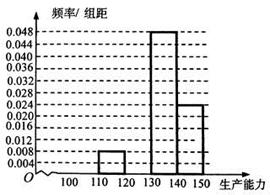
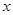 、
、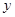 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;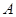 类工人和
类工人和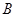 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
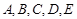 五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为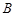 的考生有
的考生有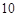 人.
人. 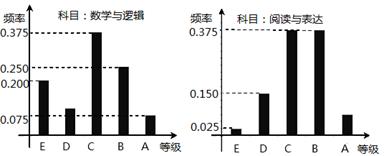
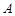 的人数;
的人数; 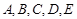 分别对应
分别对应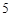 分,
分,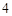 分,
分,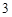 分,
分,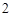 分,
分,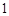 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分; 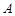 . 在至少一科成绩为
. 在至少一科成绩为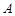 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为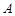 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
| | 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | |
| | 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
| 区间 | [10,20) | [20,30) | [30,40] |
| 人数 | | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
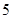 次试验,根据收集到
次试验,根据收集到 ,利用下表中数据推断
,利用下表中数据推断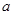 的值为( )
的值为( )零件数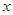 (个) (个) | 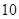 | 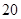 | 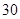 | 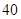 | 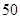 |
加工时间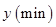 | 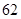 | 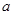 |  | 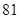 | 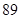 |
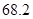 B.
B.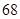 C.
C.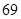 D.
D.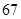
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =
= +
+ x,求得
x,求得 =0.51,
=0.51, =61.75,
=61.75, =38.14,则线性回归方程为________.
=38.14,则线性回归方程为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | y1 | y2 | 总计 |
| x1 | a | 40 | 94 |
| x2 | 32 | 63 | 95 |
| 总计 | 86 | b | 189 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com