
【题目】函数f(x)= ![]() (x2﹣9)的单调递增区间为( )
(x2﹣9)的单调递增区间为( )
A.(0,+∞)
B.(﹣∞,0)
C.(3,+∞)
D.(﹣∞,﹣3)
【答案】D
【解析】解:由x2﹣9>0解得x>3或x<﹣3,即函数的定义域为{x|x>3或x<﹣3},
设t=x2﹣9,则函数y= ![]() t为减函数,
t为减函数,
根据复合函数单调性之间的关系知要求函数f(x)的单调递增区间,
即求函数t=x2﹣9的递减区间,
∵t=x2﹣9,递减区间为(﹣∞,﹣3),
则函数f(x)的递增区间为(﹣∞,﹣3),
故选:D
【考点精析】解答此题的关键在于理解函数的单调性的相关知识,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种,以及对复合函数单调性的判断方法的理解,了解复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a∈R,若对任意的非零的实数x1 , 存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的最小值为( )
,其中a∈R,若对任意的非零的实数x1 , 存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的最小值为( )
A.![]()
B.5
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)判断并证明函数f(x)的奇偶性
(2)判断并证明当x∈(﹣1,1)时函数f(x)的单调性;
(3)在(2)成立的条件下,解不等式f(2x﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】100名学生报名参加A、B两个课外活动小组,报名参加A组的人数是全体学生人数的 ![]() ,报名参加B组的人数比报名参加A组的人数多3,两组都没报名的人数是同时报名参加A、B两组人数的
,报名参加B组的人数比报名参加A组的人数多3,两组都没报名的人数是同时报名参加A、B两组人数的 ![]() 多1,求同时报名参加A、B两组人数( )
多1,求同时报名参加A、B两组人数( )
A.36
B.13
C.24
D.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和![]() 分别为
分别为![]() 与
与![]() 的中点,对于常数
的中点,对于常数![]() ,在梯形
,在梯形![]() 的四条边上恰好有8个不同的点
的四条边上恰好有8个不同的点![]() ,使得
,使得![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
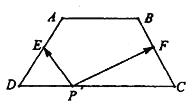
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( ) 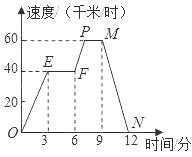
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com