
【题目】已知函数![]() ,
,![]() ,且
,且![]() 在
在![]() 处取得极大值1.
处取得极大值1.
(1)求a,b的值;
(2)当![]() 时,
时,![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
科目:高中数学 来源: 题型:
【题目】一种新的验血技术可以提高血液检测效率.现某专业检测机构提取了![]() 份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中
份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中![]() 份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这
份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这![]() 份血液再逐一检测,直到确定呈阳性的血液为止.
份血液再逐一检测,直到确定呈阳性的血液为止.
(1)若![]() ,求恰好经过3次检测而确定呈阳性的血液的事件概率;
,求恰好经过3次检测而确定呈阳性的血液的事件概率;
(2)若![]() ,宜采用以上方案检测而确定呈阳性的血液所需次数为
,宜采用以上方案检测而确定呈阳性的血液所需次数为![]() ,
,
①求![]() 的概率分布;
的概率分布;
②求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国北斗卫星导航系统是中国自行研制的全球卫星导航系统,预计2020年北斗全球系统建设将全面完成.如图是在室外开放的环境下,北斗二代和北斗三代定位模块,分别定位的50个点位的横、纵坐标误差的值,其中“![]() ”表示北斗二代定位模块的误差的值,“+”表示北斗三代定位模块的误差的值.(单位:米)
”表示北斗二代定位模块的误差的值,“+”表示北斗三代定位模块的误差的值.(单位:米)
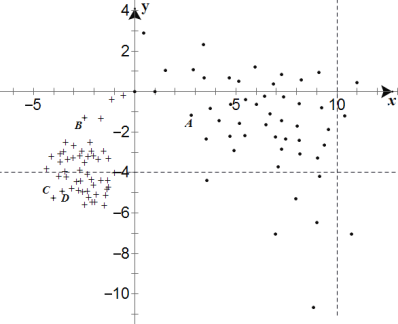
(Ⅰ)从北斗二代定位的50个点位中随机抽取一个,求此点横坐标误差的值大于10米的概率;
(Ⅱ)从图中A,B,C,D四个点位中随机选出两个,记X为其中纵坐标误差的值小于![]() 的点位的个数,求X的分布列和数学期望;
的点位的个数,求X的分布列和数学期望;
(Ⅲ)试比较北斗二代和北斗三代定位模块纵坐标误差的方差的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将长方形OAA1O1(及其内部)绕OO1旋转一周形成圆柱,其中![]() ,弧
,弧![]() 的长为
的长为![]() ,AB为⊙O的直径.
,AB为⊙O的直径.
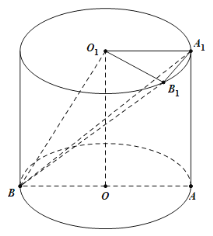
(1)在弧![]() 上是否存在点
上是否存在点![]() (
(![]() ,
,![]() 在平面
在平面![]() 的同侧),使
的同侧),使![]() ,若存在,确定其位置,若不存在,说明理由.
,若存在,确定其位置,若不存在,说明理由.
(2)求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若向量列![]() ,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即
,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即![]() (
(![]() ,且
,且![]() ,
,![]() 为常向量),则称这个向量列
为常向量),则称这个向量列![]() 为等差向量列,这个常向量叫做等差向量列的公差,且向量列
为等差向量列,这个常向量叫做等差向量列的公差,且向量列![]() 的前
的前![]() 项和为
项和为![]() .已知等差向量列
.已知等差向量列![]() 满足
满足![]() ,则向量列
,则向量列![]() 的前
的前![]() 项和
项和![]() ( )
( )
A.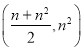 B.
B.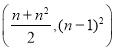
C.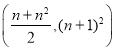 D.
D.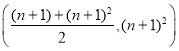
查看答案和解析>>
科目:高中数学 来源: 题型:
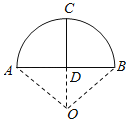
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于
,半径等于![]() 米的弧田,按照上述经验公式计算所得弧田面积约是
米的弧田,按照上述经验公式计算所得弧田面积约是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
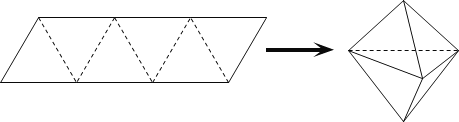
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
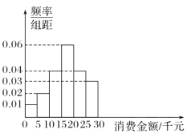
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com