Question

【题目】如图，已知AD为圆O的直径，直线BA与圆O相切于点A，直线OB与弦AC垂直并相交于点G，与弧AC相交于M，连接DC，AB=10，AC=12．
（1）求证：BADC=GCAD；
（2）求BM．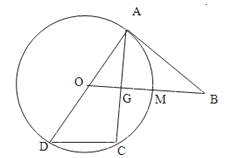

Answer 1

【答案】（1）证明：因为AC⊥OB，所以∠AGB=90°
又AD是圆O的直径，所以∠DCA=90°
又因为∠BAG=∠ADC（弦切角等于同弧所对圆周角）
所以Rt△AGB和Rt△DCA相似
所以
又因为OG⊥AC，所以GC=AG
所以，即BADC=GCAD
（2）解：因为AC=12，所以AG=6，
因为AB=10，所以
由（1）知：Rt△AGB～Rt△DCA，．所以
所以AD=15，即圆的直径2r=15
又因为AB2=BM（BM+2r），即BM2+15BM﹣100=0
解得BM=5
【解析】（1）根据AC⊥OB，及AD是圆O的直径，得到Rt△AGB和Rt△DCA相似，从而得到 ， 又GC=AG，所以 ， 从而得到证明；
（2）根据直角三角形中的边角关系求得BG，再根据直角三角形的相似及切割线定理求解即可。