
如图,已知椭圆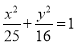 的右焦点为
的右焦点为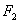 ,点
,点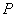 是椭圆上任意一点,圆
是椭圆上任意一点,圆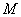 是以
是以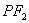 为直径的圆.
为直径的圆.
(1)若圆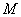 过原点
过原点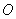 ,求圆
,求圆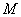 的方程;
的方程;
(2)写出一个定圆的方程,使得无论点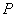 在椭圆的什么位置,该定圆总与圆
在椭圆的什么位置,该定圆总与圆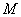 相切,请写出你的探究过程.
相切,请写出你的探究过程.

(1)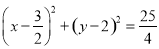 或
或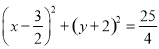 ;(2)
;(2)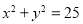 .
.
【解析】
试题分析:(1)因为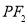 是圆
是圆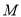 的直径,所以当圆
的直径,所以当圆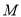 过原点
过原点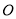 时,一定有
时,一定有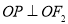 ,由此可确定点
,由此可确定点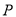 的位置并进一步求出圆
的位置并进一步求出圆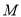 的标准方程;
的标准方程;
(2)设圆M的半径为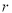 ,连结
,连结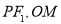 ,显然有
,显然有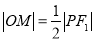
根据椭圆的标准方程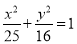 知
知 ,
,
所以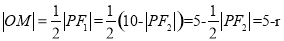
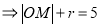 ,从而找到符合条件的定圆.
,从而找到符合条件的定圆.
【解析】
(1)解法一:因为圆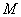 过原点
过原点 ,所以
,所以 ,所以
,所以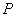 是椭圆的短轴顶点,
是椭圆的短轴顶点,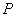 的坐标是
的坐标是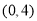 或
或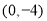 ,于是点
,于是点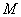 的坐标为
的坐标为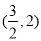 或
或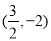 ,
,
易求圆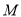 的半径为
的半径为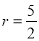
所以圆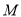 的方程为
的方程为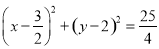 或
或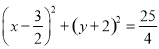 6分
6分
解法二:设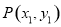 ,因为圆
,因为圆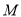 过原点
过原点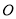 ,所以
,所以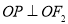
所以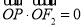 ,所以
,所以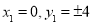 ,所以点
,所以点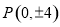
于是点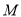 的坐标为
的坐标为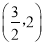 或
或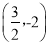 ,易求圆的半径
,易求圆的半径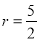
所以圆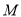 的方程为
的方程为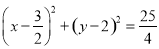 或
或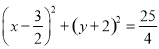 6分
6分
(2)以原点为圆心,5为半径的定圆始终与圆相内切,定圆的方程为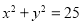 8分
8分
探究过程为:设圆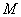 的半径为
的半径为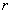 ,定圆的半径为
,定圆的半径为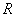 ,
,
因为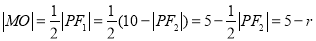 ,
,
所以当原点为定圆圆心,半径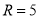 时,定圆始终与圆
时,定圆始终与圆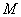 相内切. (13分)
相内切. (13分)
考点:1、椭圆的定义与标准方程;2、圆的定义与标准方程.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源:2013-2014学年河北省高三年级模拟考试理科数学试卷(解析版) 题型:解答题
在直角坐标系xOy中,直线l的参数方程为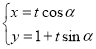 (t为参数,0≤α<π)。以原点为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为
(t为参数,0≤α<π)。以原点为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为
ρcos2θ=4sinθ。
(1)求直线l与曲线C的平面直角坐标方程;
(2)设直线l与曲线C交于不同的两点A、B,若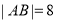 ,求α的值。
,求α的值。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三年级模拟考试文科数学试卷(解析版) 题型:选择题
方体ABCD-A1B1C1D1中,E为棱BB1的中点(如图1),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的左视图为
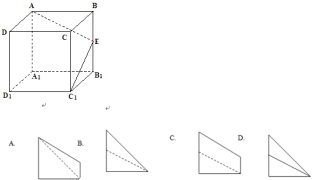
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
下列四个命题:
①利用计算机产生0~1之间的均匀随机数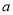 ,则事件“
,则事件“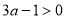 ”发生的概率为
”发生的概率为 ;
;
②“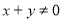 ”是“
”是“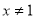 或
或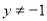 ”的充分不必要条件;
”的充分不必要条件;
③命题“在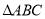 中,若
中,若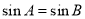 ,则
,则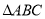 为等腰三角形”的否命题为真命题;
为等腰三角形”的否命题为真命题;
④如果平面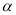 不垂直于平面
不垂直于平面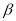 ,那么平面
,那么平面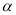 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面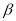 。
。
其中说法正确的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
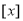 表示不超过
表示不超过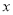 的最大整数,例如:
的最大整数,例如: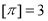 .
.
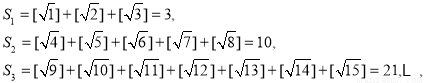
依此规律,那么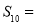 ( )
( )
A.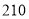 B.
B.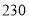 C.
C.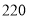 D.
D.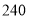
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考理科数学试卷(解析版) 题型:解答题
过双曲线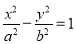
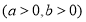 的左焦点
的左焦点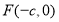
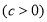 ,作倾斜角为
,作倾斜角为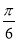 的直线
的直线 交该双曲线右支于点
交该双曲线右支于点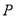 ,若
,若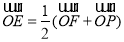 ,且
,且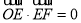 ,则双曲线的离心率为__________.
,则双曲线的离心率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com