分析:①(1)由
a1=1,an+1=(n∈N+),分别令n=1,2,3,能分别求出a
2,a
3,a
4,并由此能猜想出数列{a
n}的通项公式a
n的表达式.
(2)用数学归纳法证明能够a
n=
.
②先假设存在符合题意的常数a,b,c,再令n=1,n=2,n=3构造三个方程求出a,b,c,再用用数学归纳法证明成立,证明时先证:(1)当n=1时成立.(2)再假设n=k(k≥1)时,成立,即1•2
2+2•3
2++k(k+1)
2=
(3k
2+11k+10),再递推到n=k+1时,成立即可.
解答:解:①(1)∵
a1=1,an+1=(n∈N+),
∴
a2==
,
a3==
,
a4==
.
∴猜想数列{a
n}的通项公式a
n=
.
(2)用数学归纳法证明a
n=
.
当n=1时,
a1==
,成立.
假设当n=k时,a
n=
成立,即
ak=.
则当n=k+1时,a
k+1=
=
=
=
=
,也成立.
故a
n=
.
②证明:假设存在符合题意的常数a,b,c,
在等式1•2
2+2•3
2++n(n+1)
2=
(an
2+bn+c)中,
令n=1,得4=
(a+b+c)①
令n=2,得22=
(4a+2b+c)②
令n=3,得70=9a+3b+c③
由①②③解得a=3,b=11,c=10,
于是,对于n=1,2,3都有
1•2
2+2•3
2++n(n+1)
2=
(3n
2+11n+10)(*)成立.
下面用数学归纳法证明:对于一切正整数n,(*)式都成立.
(1)当n=1时,由上述知,(*)成立.
(2)假设n=k(k≥1)时,(*)成立,
即1•2
2+2•3
2++k(k+1)
2=
•(3k
2+11k+10),
那么当n=k+1时,
1•2
2+2•3
2++k(k+1)
2+(k+1)(k+2)
2=
(3k
2+11k+10)+(k+1)(k+2)
2=
(3k
2+5k+12k+24)
=
[3(k+1)
2+11(k+1)+10],
由此可知,当n=k+1时,(*)式也成立.
综上所述,当a=3,b=11,c=10时题设的等式对于一切正整数n都成立.
点评:第①题主要考查递推公式的应用,第②题主要考查研究存在性问题和数学归纳法,对存在性问题先假设存在,再证明是否符合条件.数学归纳法的关键是递推环节,要符合假设的模型才能成立.



 只以甲题计分)
只以甲题计分)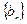 的前
的前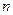 项和为
项和为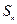 ,且
,且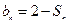 ;数列
;数列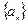 为等差数列,且
为等差数列,且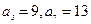
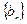 的通项公式
的通项公式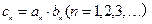 ,
,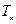 为数列
为数列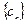 的前
的前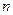
 项和,求
项和,求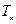
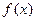 ,已知当
,已知当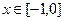 时,
时,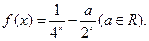
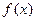 在[0,1]上的最大值
在[0,1]上的最大值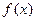 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数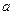 的取值范围
的取值范围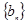 的前
的前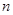 项和为
项和为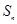 ,且
,且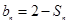 ;数列
;数列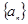 为等差数列,且
为等差数列,且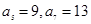
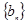 的通项公式
的通项公式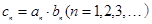 ,
, 为数列
为数列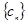 的前
的前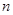 项和,求
项和,求
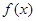 ,已知当
,已知当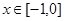 时,
时,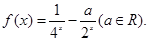
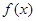 在[0,1]上的最大值
在[0,1]上的最大值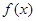 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数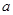 的取值范围
的取值范围