
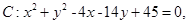 及点
及点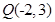 .
.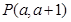 在圆上,求线段
在圆上,求线段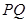 的长及直线
的长及直线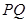 的斜率;
的斜率;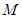 为圆
为圆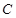 上任一点,求
上任一点,求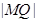 的最大值和最小值;
的最大值和最小值;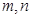 满足
满足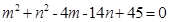 ,求
,求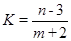 的最大值和最小值.
的最大值和最小值. (2)最小值
(2)最小值 ,最大值
,最大值 (3)
(3) 的最大值为
的最大值为 ,最小值为
,最小值为
 ,kpQ=
,kpQ=
 )2圆心C(2,7)|QC|-R≤|MQ|≤|QC|+R,因为|QC|=4
)2圆心C(2,7)|QC|-R≤|MQ|≤|QC|+R,因为|QC|=4 ,所以2
,所以2 ≤|MQ|≤6
≤|MQ|≤6 ,所以|MQ|最小值为2
,所以|MQ|最小值为2 ,最大值为6
,最大值为6
 )2,则(m,n)对应的点在以(2,7)为圆心,半径为2
)2,则(m,n)对应的点在以(2,7)为圆心,半径为2 的圆上,分析可得K=
的圆上,分析可得K= 表示该圆上的任意一点与Q(-2,3,)相连所得直线的斜率,设该直线斜率为k,则其方程为y-3=k(x+2),又由d=
表示该圆上的任意一点与Q(-2,3,)相连所得直线的斜率,设该直线斜率为k,则其方程为y-3=k(x+2),又由d= ,解得k=2±
,解得k=2± 即2-
即2- ≤K≤2+
≤K≤2+ 所以
所以 的最大值为
的最大值为 ,最小值为
,最小值为


科目:高中数学 来源:不详 题型:解答题



查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
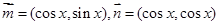 ,设函数
,设函数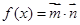
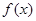 的解析式,并求最小正周期;
的解析式,并求最小正周期;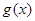 的图像是由函数
的图像是由函数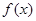 的图像向右平移
的图像向右平移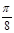 个单位得到的,求
个单位得到的,求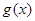 的最大值及使
的最大值及使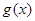 取得最大值时
取得最大值时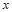 的值.
的值. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com