
| A. | S△AOC的最小值为$\frac{1}{2}$S | B. | SAOB的最小值为($\sqrt{2}$-1)S | ||
| C. | S△AOC+S△AOB的最大值为$\frac{1}{2}$S | D. | S△BOC的最大值为($\sqrt{2}$-1)S |
分析 可先证明一个结论:${S}_{△BOC}•\overrightarrow{OA}+{S}_{△AOC}•\overrightarrow{OB}+{S}_{△AOB}•\overrightarrow{OC}=\overrightarrow{0}$,可作出图形,过A作OB的平行线,交CO延长线于M,过A作OC的平行线,交BO的延长线于N,这样得到了平行四边形AMON.而根据相似三角形的比例关系,可以用$\overrightarrow{OB}$表示$\overrightarrow{AM}$,同理可用$\overrightarrow{OC}$表示$\overrightarrow{AN}$,从而得出$\overrightarrow{AO}=\frac{AF}{FB}•\overrightarrow{OB}+\frac{AD}{DC}•\overrightarrow{OC}$,这时候可以说明$\frac{{S}_{△AOC}}{{S}_{△BOC}}=\frac{AF}{FB},\frac{{S}_{△AOB}}{{S}_{△BOC}}=\frac{AD}{DC}$,这样即可得出前面的结论.从而得到${S}_{△AOC}+{S}_{△AOB}=\frac{sinα+cosα}{\sqrt{2}+sinα+cosα}•S$,这样可以说明$\frac{sinα+cosα}{\sqrt{2}+sinα+cosα}$的最大值为$\frac{1}{2}$,从而可以找出正确选项.
解答 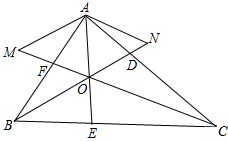 解:如图,连接AO,并延长AO交BC于D,连结BO并延长交AC于E,连结CO并延长交AB与F,过A作AM∥BD交CF延长线于M,作AN∥CF交BD延长线于N,则四边形AMON为平行四边形;
解:如图,连接AO,并延长AO交BC于D,连结BO并延长交AC于E,连结CO并延长交AB与F,过A作AM∥BD交CF延长线于M,作AN∥CF交BD延长线于N,则四边形AMON为平行四边形;
∴$\overrightarrow{AO}=\overrightarrow{AM}+\overrightarrow{AN}$;
△AMF∽△BOF;
∴$\frac{AM}{OB}=\frac{AF}{FB}$;
∴$\overrightarrow{AM}=\frac{AF}{FB}•\overrightarrow{OB}$,同理得$\overrightarrow{AN}=\frac{AD}{DC}•\overrightarrow{OC}$;
∴$\overrightarrow{AO}=\frac{AF}{FB}•\overrightarrow{OB}+\frac{AD}{DC}•\overrightarrow{OC}$;
∵△AOC与△BOC有公共的底边OC,设它们的相应的高分别为h1,h2;
则$\frac{{S}_{△AOC}}{{S}_{△BOC}}=\frac{{h}_{1}}{{h}_{2}}=\frac{AF}{FB}$,$\frac{{S}_{△AOB}}{{S}_{△BOC}}=\frac{AD}{DC}$;
∴$\overrightarrow{AO}=\frac{{S}_{△AOC}}{{S}_{△BOC}}•\overrightarrow{OB}+\frac{{S}_{△AOB}}{{S}_{△BOC}}•\overrightarrow{OC}$;
∴${S}_{△BOC}•\overrightarrow{AO}={S}_{△AOC}•\overrightarrow{OB}+{S}_{△AOB}•\overrightarrow{OC}$;
∴${S}_{△BOC}•\overrightarrow{OA}+{S}_{△AOC}•\overrightarrow{OB}+{S}_{△AOB}•\overrightarrow{OC}=\overrightarrow{0}$;
又$\sqrt{2}\overrightarrow{OA}+sinα\overrightarrow{OB}+cosα\overrightarrow{OC}=\overrightarrow{0}$;
∴${S}_{△AOC}+{S}_{AOB}=\frac{sinα+cosα}{\sqrt{2}+sinα+cosα}•S$=$\frac{sin(α+\frac{π}{4})}{sin(α+\frac{π}{4})+1}•S=[1-\frac{1}{sin(α+\frac{π}{4})+1}]•S$;
∴$α=\frac{π}{4}$时,$1-\frac{1}{sin(α+\frac{π}{4})+1}$取最大值$\frac{1}{2}$;
∴S△AOC+S△AOB的最大值为$\frac{1}{2}S$.
故选C.
点评 考查向量加法的平行四边形法则,相似三角形的对应边的比例关系,向量数乘的几何意义,以及三角形的面积公式,两角和的正弦公式,分离常数法的运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 930 | B. | 1520 | C. | 60 | D. | 61 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )| A. | $\frac{{20\sqrt{2}}}{3}$ | B. | $\frac{{20\sqrt{3}}}{3}$ | C. | $\frac{{50\sqrt{2}}}{9}$ | D. | $\frac{{50\sqrt{3}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | [$\frac{6}{5}$,6) | C. | [1,$\frac{6}{5}$] | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
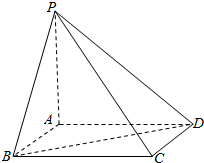 在四棱锥P-ABCD中:ABCD是正方形,PA⊥平面ABCD,PA=AB=a.
在四棱锥P-ABCD中:ABCD是正方形,PA⊥平面ABCD,PA=AB=a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com