Question

【题目】如图,直线与抛物线交于A、B两点,线段AB的垂直平分线与直线y=－5交于Q点.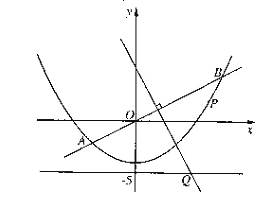

（1）求点Q的坐标；
（2）当P为抛物线上位于线段AB下方（含A、B）的动点时,求ΔOPQ面积的最大值.

Answer 1

【答案】
（1）

【解答】解方程组 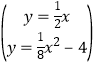得 或

即A(－4,－2),B(8,4),从而AB的中点为M(2,1).由kAB= ,直线AB的垂直平分线方程

y－1= (x－2).令y=－5,得x=5,∴Q(5,－5)．

（2）

【解答】直线OQ的方程为x+y=0,设P(x, x2－4).∵点P到直线OQ的距离 ,

,

∴.

∵P为抛物线上位于线段AB下方的点,且P不在直线OQ上,∴－4≤x<4 －4或4 －4<x≤8.

∵函数y=x2+8x－32在区间[－4,8]上单调递增,∴当x=8时,ΔOPQ的面积取到最大值30．

【解析】（1）把直线方程抛物线方程联立求得交点A，B的坐标，则AB中点M的坐标可得，利用AB的斜率推断出AB垂直平分线的斜率，进而求得AB垂直平分线的方程，把y=-5代入求得Q的坐标．（2）设出P的坐标，利用P到直线0Q的距离求得三角形的高，利用两点间的距离公式求得QO的长，最后利用三角形面积公式表示出三角形OPQ，利用x的范围和二次函数的单调性求得三角形面积的最大值．