
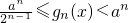
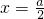 ,由下表:
,由下表:
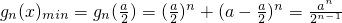
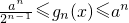 .
.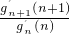 >n+1,而g2′(2)=2[22-1-(2-a)2-1]=2a
>n+1,而g2′(2)=2[22-1-(2-a)2-1]=2a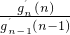 •
•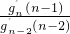 …
…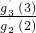 •g2′(2)>n×(n-1)×…×3×2a=n!a,
•g2′(2)>n×(n-1)×…×3×2a=n!a, ,进而得到函数的最值,即可以得到函数的值域.
,进而得到函数的最值,即可以得到函数的值域.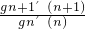 >n+1,(*),根据(*)式可以构造等式gn′(n)=
>n+1,(*),根据(*)式可以构造等式gn′(n)=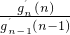 •
•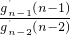 …
…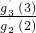 •g2′(2)>n×(n-1)×…×3×2a=n!a,又g2′(2)=2[22-1-(2-a)2-1]=2!a,故n≥2,n∈N时,有gn′(n)≥n!a
•g2′(2)>n×(n-1)×…×3×2a=n!a,又g2′(2)=2[22-1-(2-a)2-1]=2!a,故n≥2,n∈N时,有gn′(n)≥n!a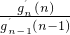 •
•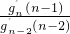 …
…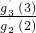 •g2′(2),进而得到结果.这道题的结论中出现n!,这时我们要能够想到构造类似的等式,这都是平时的总结经验,只有平时多总结、探索,才能在实战中,做到举一反三.
•g2′(2),进而得到结果.这道题的结论中出现n!,这时我们要能够想到构造类似的等式,这都是平时的总结经验,只有平时多总结、探索,才能在实战中,做到举一反三. 

科目:高中数学 来源: 题型:
| an | 2n-1 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年四川省成都市石室中学高三(上)8月月考数学试卷(理科)(解析版) 题型:解答题
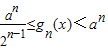
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com