
分析 根据条件求出命题的成立的等价条件,根据复合命题真假关系进行判断即可.
解答 解:若:?x≥1,x-$\frac{a}{x}$+2≥0,即x+2≥$\frac{a}{x}$,
即x2+2x≥a在x≥1时成立,
设f(x)=x2+2x,则f(x)=(x+1)2-1,
当x≥1时,函数f(x)为增函数,则函数f(x)的最小值为f(1)=1+2=3,
则a≤3,即p:a≤3
若点P(1,1)在圆(x-a)2+(y-a)2=4的外部,
则(1-a)2+(1-a)2>4,
即(a-1)2>2,即a>1+$\sqrt{2}$或a<1-$\sqrt{2}$,
若存在正数a,使得p∨q为真命题;p∧q假命题,
则p,q为一真一假,
则此时p:0<a≤3,q:a>1+$\sqrt{2}$,
若p真q假,则$\left\{\begin{array}{l}{0<a≤3}\\{0<a≤1+\sqrt{2}}\end{array}\right.$,得0<a≤1+$\sqrt{2}$,
若p假q真,则$\left\{\begin{array}{l}{a>3}\\{a>1+\sqrt{2}}\end{array}\right.$,得a>3,
综上0<a≤1+$\sqrt{2}$或a>3.
点评 本题主要考查复合命题真假的应用,根据条件求出命题的等价条件是解决本题的关键.


科目:高中数学 来源: 题型:解答题
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | 20 | 40 | 70 | 50 | 20 | 200 |
| 女生 | 男生 | 总计 | |
| 及格人数 | 60 | ||
| 不及格人数 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
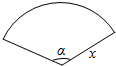 如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.
如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
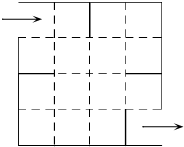 有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com