
【题目】某校参加夏令营的同学有3名男同学![]() 和3名女同学
和3名女同学![]() ,其所属年级情况如下表:
,其所属年级情况如下表:
高一年级 | 高二年级 | 高三三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母写出这个试验的样本空间;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件![]() 的样本点,并求事件
的样本点,并求事件![]() 发生的概率.
发生的概率.
科目:高中数学 来源: 题型:
【题目】(东北三省四市教研联合体2018届高三第二次模拟考试)中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”取意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算.算筹是将几寸长的小竹棍摆在下面上进行运算.算筹的摆放形式有纵横两种形式(如下图所示).表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列.但各位数码的筹式要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位数用横式表示.依此类推.例如3266用算筹表示就是![]() ,则8771用算筹可表示为
,则8771用算筹可表示为
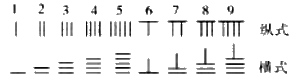
中国古代的算筹数码
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解学生对电子竞技的兴趣,从该校高二年级的学生中随机抽取了![]() 人进行检查,已知这
人进行检查,已知这![]() 人中有
人中有![]() 名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有
名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有![]() 的人对电子竞技有兴趣.
的人对电子竞技有兴趣.
![]() 在被抽取的女生中与
在被抽取的女生中与![]() 名高二
名高二![]() 班的学生,其中有
班的学生,其中有![]() 名女生对电子产品竞技有兴趣,先从这
名女生对电子产品竞技有兴趣,先从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求其中至少有
人,求其中至少有![]() 人对电子竞技有兴趣的概率;
人对电子竞技有兴趣的概率;
![]() 完成下面的
完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“电子竞技的兴趣与性别有关”.
的把握认为“电子竞技的兴趣与性别有关”.
有兴趣 | 没兴趣 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考数据:
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家报刊销售点从报社买进报纸的价格是每份0.35元,卖出的价格是每份0.50元,卖不掉的报纸还可以每份0.08元的价格退回报社.在一个月(30天)里,有20天每天可以卖出400份,其余10天每天只能卖出250份.设每天从报社买进的报纸的数量相同,则应该每天从报社买进多少份,才能使每月所获得的利润最大?并计算该销售点一个月最多可赚得多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)求过点![]() 和函数
和函数![]() 的图像相切的直线方程;
的图像相切的直线方程;
(2)若对任意![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若存在唯一的整数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=AA1=1,![]() , AB1与A1B相交于点D,M为B1C1的中点 .
, AB1与A1B相交于点D,M为B1C1的中点 .

(1)求证:CD⊥平面BDM;
(2)求平面B1BD与平面CBD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
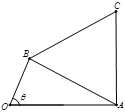
【题目】已知函数![]()
![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;如图,四边形
上单调递减;如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的内角
的内角![]() 的对边,
的对边,
且满足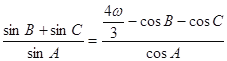 .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,设
,设![]() ,
,![]() ,
,
![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com