
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() 且
且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明: ![]() <0.
<0.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,理由见解析
,理由见解析
【解析】试题分析:(1)![]() ,可知
,可知![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)
,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2) ![]() 在区间
在区间![]() 上为单调递增函数,即
上为单调递增函数,即![]() 在
在![]() 上恒成立。
上恒成立。![]() ,利用分离参数
,利用分离参数![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最大值。
的最大值。
(3)![]() 有两个实根
有两个实根![]() ,
, ![]() ,两式相减
,两式相减![]() ,又
,又![]() ,
, ![]()
![]() .要证:
.要证: ![]() ,只需证:
,只需证:![]() ,令
,令![]() 可证。
可证。
试题解析:(1) ![]()
函数![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,
,1]是增函数,在[1,2]是减函数,
所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
因为![]() 在区间
在区间![]() 单调递增函数,所以
单调递增函数,所以![]() 在(0,3)恒成立
在(0,3)恒成立
![]() ,有
,有![]() =
=![]() ,(
,(![]() )
)
综上: ![]()
(3)∵![]() ,又
,又![]() 有两个实根
有两个实根![]() ,
,
∴![]() ,两式相减,得
,两式相减,得![]() ,
,
∴![]() ,
,
于是![]()
![]() .
.
![]()
要证: ![]() ,只需证:
,只需证:![]()
只需证:![]() .(*)
.(*)
令![]() ,∴(*)化为
,∴(*)化为 ![]() ,只证
,只证![]() 即可.
即可.
![]() 在(0,1)上单调递增,
在(0,1)上单调递增,![]() ,
,
即![]() .∴
.∴![]() .
.
(其他解法根据情况酌情给分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最后一位选手的成绩.
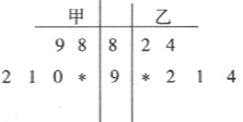
(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.请你从平均分和方差的角度来分析两个班的选手的情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(I)写出直线![]() 的一般方程与曲线
的一般方程与曲线![]() 的直角坐标方程,并判断它们的位置关系;
的直角坐标方程,并判断它们的位置关系;
(II)将曲线![]() 向左平移
向左平移![]() 个单位长度,向上平移
个单位长度,向上平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]() ,设曲线
,设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|-2≤x≤10},Q={x|1-m≤x≤1+m}.
(1)求集合RP;
(2)若PQ,求实数m的取值范围;
(3)若P∩Q=Q,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
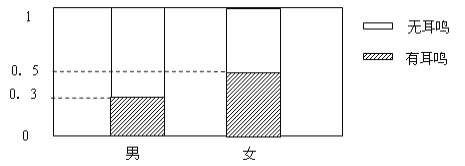
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附:![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一数集的任一元素的倒数仍在该集合中,则称该数集为“可倒数集”.
(1)判断集合A={-1,1,2}是否为可倒数集;
(2)试写出一个含3个元素的可倒数集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了调查喜欢语文学科与性别的关系,随机调查了一些学生情况,具体数据如下表:
调查统计 | 不喜欢语文 | 喜欢语文 |
男 | 13 | 10 |
女 | 7 | 20 |
为了判断喜欢语文学科是否与性别有关系,根据表中的数据,得到K2的观测值
k=![]() ≈4.844,因为k≥3.841,根据下表中的参考数据:
≈4.844,因为k≥3.841,根据下表中的参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
判定喜欢语文学科与性别有关系,那么这种判断出错的可能性为( )
A. 95% B. 50% C. 25% D. 5%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com