
【题目】已知△ABC是锐角三角形,cos22A+sin2A=1.
(Ⅰ)求角A;
(Ⅱ)若BC=1,B=x,求△ABC的周长f(x)的单调区间.
【答案】(Ⅰ)![]() ;(Ⅱ) 单调增区间是(0,
;(Ⅱ) 单调增区间是(0,![]() ],单调减区间是[
],单调减区间是[![]() ,
,![]() ).
).
【解析】
试题分析:(Ⅰ)由已知cos22A+sin2A=1,把左边的一项移到右边,应用同角关系式化简,再用二倍角公式变形,可求得A角;(Ⅱ)由正弦定理求出另两边长,得周长![]() ,由两角和的正弦公式化
,由两角和的正弦公式化![]() 为一个三角函数形式,再由正弦函数的单调性可得单调区间,求解时要注意函数的定义域.
为一个三角函数形式,再由正弦函数的单调性可得单调区间,求解时要注意函数的定义域.
试题解析:(Ⅰ)∵cos22A+sin2A=1,
∴cos22A=cos2A∴cos2A=±cosA,∴2cos2A﹣1±cosA=0,
∵△ABC是锐角三角形,∴cosA=![]() ,∴A=
,∴A=![]() .
.
(Ⅱ)∵BC=1,B=x,
∴AC=![]() sinx,AB=cosx+
sinx,AB=cosx+![]() sinx,
sinx,
∴△ABC的周长f(x)=1+cosx+![]() sinx=1+2sin(x+
sinx=1+2sin(x+![]() ),
),
∴当﹣![]() +2kπ≤x+
+2kπ≤x+![]() ≤
≤![]() +2kπ,(k∈Z)时,x∈[﹣
+2kπ,(k∈Z)时,x∈[﹣![]() +2kπ,
+2kπ,![]() +2kπ],
+2kπ],
∵x∈(0,![]() )∴f(x)的单调增区间是(0,
)∴f(x)的单调增区间是(0,![]() ],单调减区间是[
],单调减区间是[![]() ,
,![]() ).
).


科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润W(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在数列{an}中,Sn为其前n项和,若an>0,且4Sn=an2+2an+1(n∈N*),数列{bn}为等比数列,公比q>1,b1=a1,且2b2,b4,3b3成等差数列.
(1)求{an}与{bn}的通项公式;
(2)令cn=![]() ,若{cn}的前项和为Tn,求证:Tn<6.
,若{cn}的前项和为Tn,求证:Tn<6.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)记![]() ,求证:函数
,求证:函数![]() 在区间
在区间![]() 内有且仅有一个零点;
内有且仅有一个零点;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,若关于
,若关于![]() 的方程
的方程![]() (其中
(其中![]() 为常数)在区间
为常数)在区间![]() 有两个不相等的实根
有两个不相等的实根![]() ,记
,记![]() 在
在![]() 内的零点为
内的零点为![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 的图象在点
的图象在点![]() 处的切线的倾斜角为
处的切线的倾斜角为![]() ,且函数
,且函数![]() 当且仅当在
当且仅当在![]() 处取得极值,其中
处取得极值,其中![]() 为
为![]() 的导函数,求
的导函数,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
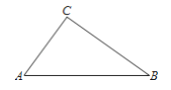
【题目】如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为![]() (单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设
(单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设![]() 时,乙到达C地.
时,乙到达C地.
(1)求![]() 与
与![]() 的值;
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当![]() 时,求
时,求![]() 的表达式,并判断
的表达式,并判断![]() 在
在![]() 上的最大值是否超过3?并说明理由.
上的最大值是否超过3?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() :
: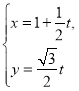 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,
,![]() 为常数,
为常数, ![]() .
.
(1)求![]() 的值;(2)若
的值;(2)若![]() 在
在![]() 上为单调函数,求
上为单调函数,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若在
,若在![]() 上至少存在一个
上至少存在一个![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com