
【题目】定义在R上的偶函数y=f(x),当x≥0时,f(x)=x2﹣2x. 
(1)求当x<0时,函数y=f(x)的解析式,并在给定坐标系下,画出函数y=f(x)的图象;
(2)写出函数y=|f(x)|的单调递减区间.
【答案】
(1)解:设x<0,则﹣x>0,
∵y=f(x)是R上的偶函数,
∴f(x)=f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x,
即当x<0时,f(x)=x2+2x.
图象如下图所示:

(2)解:将y=f(x)图象在x轴下方的部分翻折到上方可得y=|f(x)|的图象.
由图象知,函数y=|f(x)|的单调递减区间是:(﹣∞,﹣2],[﹣1,0],[1,2]
【解析】(1)根据函数的奇偶性求出函数f(x)的解析式,从而画出f(x)的图象即可;(2)根据函数的图象求出y=|f(x)|的递减区间即可.
【考点精析】利用函数的单调性对题目进行判断即可得到答案,需要熟知注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ) 求曲线![]() 与
与![]() 交点的平面直角坐标;
交点的平面直角坐标;
(Ⅱ) 点![]() 分别在曲线
分别在曲线![]() ,
, ![]() 上,当
上,当![]() 最大时,求
最大时,求![]() 的面积(
的面积(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次函数f(x)是R上的增函数,已知f[f(x)]=16x+5,g(x)=f(x)(x+m).
(1)求f(x);
(2)若g(x)在(1,+∞)单调递增,求实数m的取值范围;
(3)当x∈[﹣1,3]时,g(x)有最大值13,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3.定义在R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0<x<1},则A中所有元素之和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间![]() (单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
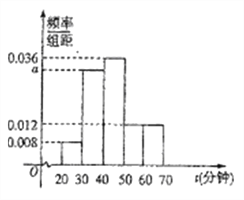
(1)求![]() 的值;
的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为![]() ,
, ![]() 的两组中各抽取多少人?
的两组中各抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
比较关注 | 不太关注 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:![]() ,
,![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,定义x≥0时,f(x)= ![]()
(1)求f(﹣2);
(2)当x<﹣3时,求f(x)的解析式;
(3)设函数y=f(x)在区间[﹣5,5]上的最大值为g(a),试求g(a)的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com