
 ,+∞)
,+∞)
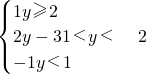 ,做出函数的图象,结合图象可知函数的最大值1,由a>|y-1|-|y-2|(y∈R)恒成立?a>g(y)max 从而可得a>1然后求出函数f(x)=loga(x2-5x+6)的定义域为{x|x>3,或x<2},由t=x2-5x+6及y=logat的单调性结合复合函数的单调性可1求函数f(x)单调递减区间
,做出函数的图象,结合图象可知函数的最大值1,由a>|y-1|-|y-2|(y∈R)恒成立?a>g(y)max 从而可得a>1然后求出函数f(x)=loga(x2-5x+6)的定义域为{x|x>3,或x<2},由t=x2-5x+6及y=logat的单调性结合复合函数的单调性可1求函数f(x)单调递减区间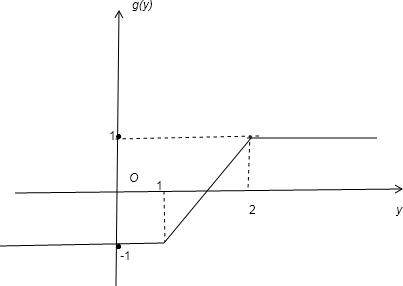 解:令g(y)=|y-1|-|y-2|=
解:令g(y)=|y-1|-|y-2|=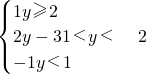 则函数的图象如下图,由图可知函数的最大值1
则函数的图象如下图,由图可知函数的最大值1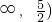 ,
,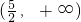 要注意函数的单调区间一定要在函数有意义的条件下讨论.
要注意函数的单调区间一定要在函数有意义的条件下讨论. 

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
A、(
| ||
| B、(3,+∞) | ||
C、(-∞,
| ||
| D、(-∞,2) |
查看答案和解析>>
科目:高中数学 来源:江西省师大附中2012届高三上学期期中考试数学理科试题 题型:013
若实数a满足a>|y-1|-|y-2|(y∈R)恒成立,则函数f(x)=loga(x2-5x+6)的单调减区间为
(![]() ,+∞)
,+∞)
(3,+∞)
(-∞,![]() )
)
(-∞,2)
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.(
| B.(3,+∞) | C.(-∞,
| D.(-∞,2) |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年吉林省长春市东北师大附中高三(上)第三次摸底数学试卷(解析版) 题型:选择题
 ,+∞)
,+∞)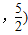
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com