
【题目】如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图2所示.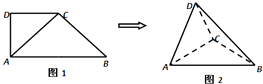
(1)求证:BC⊥平面ACD;
(2)求几何体D﹣ABC的体积.
【答案】
(1)
证明:
【证法一】:在图1中,由题意知, ![]() ,∴AC2+BC2=AB2,∴AC⊥BC
,∴AC2+BC2=AB2,∴AC⊥BC
取AC中点O,连接DO,则DO⊥AC,又平面ADC⊥平面ABC,
且平面ADC∩平面ABC=AC,DO平面ACD,从而OD⊥平面ABC,
∴OD⊥BC
又AC⊥BC,AC∩OD=O,
∴BC⊥平面ACD
【证法二】:在图1中,由题意,得 ![]() ,∴AC2+BC2=AB2,∴AC⊥BC
,∴AC2+BC2=AB2,∴AC⊥BC
∵平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC面ABC,∴BC⊥平面ACD
(2)
解:由(1)知,BC为三棱锥B﹣ACD的高,且 ![]() ,S△ACD=
,S△ACD= ![]() ×2×2=2,
×2×2=2,
所以三棱锥B﹣ACD的体积为: ![]() ,
,
由等积性知几何体D﹣ABC的体积为: ![]() .
.
【解析】(1)解法一:由题中数量关系和勾股定理,得出AC⊥BC,再证BC垂直与平面ACD中的一条直线即可,△ADC是等腰Rt△,底边上的中线OD垂直底边,由面面垂直的性质得OD⊥平面ABC,所以OD⊥BC,从而证得BC⊥平面ACD;
解法二:证得AC⊥BC后,由面面垂直,得线面垂直,即证.(2),由高和底面积,求得三棱锥B﹣ACD的体积即是几何体D﹣ABC的体积.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,以椭圆的四个顶点为顶点的四边形的面积为8.
,以椭圆的四个顶点为顶点的四边形的面积为8.
(Ⅰ)求椭圆![]() 的方程;
的方程;
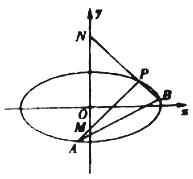
(Ⅱ)如图,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.若
的左上方.若![]() ,且直线
,且直线![]() ,
, ![]() 分别与
分别与![]() 轴交于
轴交于![]() ,
, ![]() 点,求线段
点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
)x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为:②③.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:f(x)=2 ![]() cos2x+sin2x﹣
cos2x+sin2x﹣ ![]() +1(x∈R).求:
+1(x∈R).求:
(1)f(x)的最小正周期;
(2)f(x)的单调增区间;
(3)若x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌茶壶的原售价为80元/个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下方法促销:如果只购买一个茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;…,一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个;乙店一律按原价的75%销售.现某茶社要购买这种茶壶x个,如果全部在甲店购买,则所需金额为y1元;如果全部在乙店购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)该茶社去哪家茶具店购买茶壶花费较少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n∈R,定义在区间[m,n]上的函数f(x)=log2(4﹣|x|)的值域是[0,2],若关于t的方程( ![]() )|t|+m+1=0(t∈R)有实数解,则m+n的取值范围是 .
)|t|+m+1=0(t∈R)有实数解,则m+n的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com